【题目】模型与应用.
(模型)
(1)如图①,已知AB∥CD,求证∠1+∠MEN+∠2=360°.

(应用)
(2)如图②,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6的度数为 .

如图③,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为 .

(3)如图④,已知AB∥CD,∠AM1M2的角平分线M1 O与∠CMnMn-1的角平分线MnO交于点O,若∠M1OMn=m°.

在(2)的基础上,求∠2+∠3+∠4+∠5+∠6+……+∠n-1的度数.(用含m、n的代数式表示)
参考答案:
【答案】(1)证明见解析;(2)900° ,180°(n-1);(3)(180n-180-2m)°
【解析】(1)过点E作EF∥CD,根据平行于同一直线的两条直线互相平行可得EF∥AB,根据两直线平行,同旁内角互补可得∠1+∠MEF=180°,∠2+∠NEF=180°,即可得∠1+∠2+∠MEN=360° ;(2)①分别过E点,F点,G点,H点作L1,L2,L3,L4平行于AB,利用(1)的方法可得∠1+∠2+∠3+∠4+∠5+∠6=180×5=900°;②由上面的解题方法可得答案;(3)过点O作SR∥AB,根据平行于同一直线的两条直线互相平行可得SR∥CD,根据两直线平行,内错角相等可得∠AM1O=∠M1OR,∠C MnO=∠MnOR,所以∠A M1O+∠CMnO=∠M1OR+∠MnOR,即可得∠A M1O+∠CMnO=∠M1OMn=m°,根据角平分线的定义可得∠AM1M2=2∠A M1O,∠CMnMn-1=2∠CMnO,由此可得∠AM1M2+∠CMnMn-1=2∠AM1O+2∠CMnO=2∠M1OMn=2m°,又因∠A M1E+∠2+∠3+∠4+∠5+∠6+……+∠n-1+∠CMnMn-1=180°(n-1),由此可得
∠2+∠3+∠4+∠5+∠6+…+∠n-1=(180n-180-2m)°.
【模型】
(1)如图①,已知AB∥CD,求证∠1+∠2+∠MEN=360°.
证明:过点E作EF∥CD,
∵AB∥CD,
∴EF∥AB,
∴∠1+∠MEF=180°,
同理∠2+∠NEF=180°
∴∠1+∠2+∠MEN=360°
【应用】
(2)900° , 180°(n-1)
分别过E点,F点,G点,H点作L1,L2,L3,L4平行于AB,利用(1)的方法可得∠1+∠2+∠3+∠4+∠5+∠6=180×5=900°;

由上面的解题方法可得:∠1+∠2+∠3+∠4+∠5+∠6+…+∠n=180°(n-1);
(3)过点O作SR∥AB,

∵AB∥CD,
∴SR∥CD,
∴∠AM1O=∠M1OR
同理∠C MnO=∠MnOR
∴∠A M1O+∠CMnO=∠M1OR+∠MnOR,
∴∠A M1O+∠CMnO=∠M1OMn=m°,
∵M1O平分∠AM1M2,
∴∠AM1M2=2∠A M1O,
同理∠CMnMn-1=2∠CMnO,
∴∠AM1M2+∠CMnMn-1=2∠AM1O+2∠CMnO=2∠M1OMn=2m°,
又∵∠A M1E+∠2+∠3+∠4+∠5+∠6+……+∠n-1+∠CMnMn-1=180°(n-1),
∴∠2+∠3+∠4+∠5+∠6+…+∠n-1=(180n-180-2m)°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生社团为了解本校学生喜欢球类运动的情况,随机抽取了若干名学生进行问卷调查,要求每位学生只能填写一种自己喜欢的球类运动,并将调查的结果绘制成如下的两幅不完整的统计图.
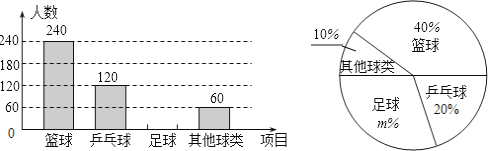
请根据统计图表提供的信息,解答下列问题:
(1)参加调查的人数共有△人;在扇形图中,m=△;将条形图补充完整;
(2)如果该校有3500名学生,则估计喜欢“篮球”的学生共有多少人?
(3)该社团计划从篮球、足球和乒乓球中,随机抽取两种球类组织比赛,请用树状图或列表法,求抽取到的两种球类恰好是“篮球”和“足球”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中
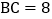 ,
,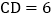 ,将
,将 沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是
沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是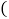
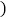

A. 3 B.
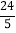 C. 5 D.
C. 5 D. 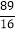
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图,

∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
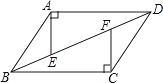
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一张直角三角形纸片ABC,边
 ,
, ,
,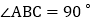 ,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为
,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为


A. 16 B. 17 C. 18 D. 19
相关试题

