Question

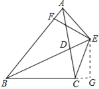
【题目】已知：如图，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足，下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=EF=EC；④BA+BC=2BF，其中正确的结论有________（填序号）．

Answer 1

【答案】①②④

【解析】

易证△ABD≌△EBC，可得∠BCE=∠BDA，AD=EC可得①②正确，再根据角平分线的性质可求得∠DAE=∠DCE，即AD=AE=EC，根据AD=AE=EC可求得④正确

解：①∵BD为△ABC的角平分线，
∴∠ABD=∠CBD，
在△ABD和△EBC中，

,

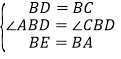∴△ABD≌△EBC（SAS），
∴①正确；
②∵BD为△ABC的角平分线，BD=BC，BE=BA，
∴∠BCD=∠BDC=∠BAE=∠BEA，
∵△ABD≌△EBC，
∴∠BCE=∠BDA，
∴∠BCE+∠BCD=∠BDA+∠BDC=180°，
∴②正确；
③∵∠BCE=∠BDA，∠BCE=∠BCD+∠DCE，∠BDA=∠DAE+∠BEA，∠BCD=∠BEA，
∴∠DCE=∠DAE，
∴△ACE为等腰三角形，
∴AE=EC，
∵△ABD≌△EBC，
∴AD=EC，
∴AD=AE=EC，
∵BD为△ABC的角平分线，EF⊥AB，而EC不垂直与BC，
∴EF≠EC，
∴③错误；
④过E作EG⊥BC于G点，

∵E是BD上的点，∴EF=EG，
在Rt△BEG和Rt△BEF中，

,

∴Rt△BEG≌Rt△BEF（HL），
∴BG=BF，
在Rt△CEG和Rt△AFE中，

,

∴Rt△CEG≌Rt△AFE（HL），
∴AF=CG，
∴BA+BC=BF+FA+BG-CG=BF+BG=2BF，
∴④正确．
故答案为：①②④．