【题目】小国同学的父亲参加旅游团到某地旅游,准备买某种礼物送给小国.据了解,沿旅游线路依次有A、B、C三个地点可以买到此种礼物,其质量相当,价格各不相同,但不知哪家更便宜.由于时间关系,随团旅游车不会掉头行驶.
(1)若到A处就购买,写出买到最低价格礼物的概率;
(2)小国同学的父亲认为,如果到A处不买,到B处发现比A处便宜就马上购买,否则到C处购买,这样更有希望买到最低价格的礼物.这个想法是否正确?试通过树状图分析说明.
参考答案:
【答案】
(1)解:∵在每一处都有价格最低,最高,较高的可能,
∴PA处买到最低价格礼物= ![]()
(2)解:作出树状图如下:
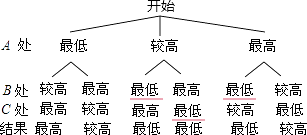
由树状图可知:P购到最低价格礼物= ![]() =
= ![]() ,
,
∵ ![]() >
> ![]() ,
,
∴他的想法是正确的
【解析】(1)分价格是最低,最高,较高三种情况,根据概率公式列式进行计算即可;(2)画出树状图,然后根据概率公式列式计算出在C处购买到最低价格礼物的概率,然后即可判断.
【考点精析】本题主要考查了列表法与树状图法的相关知识点,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ABCD的周长为36cm,过点A作AE⊥BC,AF⊥CD,垂足分别为E、F.若AE=2cm,AF=4cm.求ABCD的各边长.
-
科目: 来源: 题型:
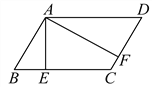
查看答案和解析>>【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】深化理解:
新定义:对非负实数x “四舍五入”到个位的值记为
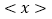 ,
,即:当n为非负整数时,如果
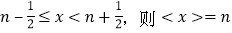 ;
;反之,当n为非负整数时,如果
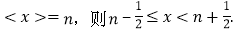
例如:<0> = <0.48> = 0,<0.64> = <1.49> = 1,<2> = 2,<3.5> = <4.12> = 4,……
试解决下列问题:
(1)填空:①
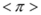 =________(
=________(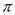 为圆周率); ②如果
为圆周率); ②如果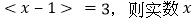 的取值范围为____________________.
的取值范围为____________________.(2)若关于x的不等式组
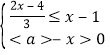 的整数解恰有3个,求a的取值范围.
的整数解恰有3个,求a的取值范围.(3)求满足
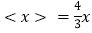 的所有非负实数x的值.
的所有非负实数x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C、D、E、F是⊙O的六等分点.
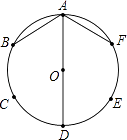
(1)连接AB、AD、AF,求证:AB+AF=AD;
(2)若P是圆周上异于已知六等分点的动点,连接PB、PD、PF,写出这三条线段长度的数量关系(不必说明理由). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
 (x>0)的图象与一次函 数y=﹣x+b的图象分别交于A(1,3)、B两点.
(x>0)的图象与一次函 数y=﹣x+b的图象分别交于A(1,3)、B两点.
(1)求m、b的值;
(2)若点M是反比例函数图象上的一动点,直线MC⊥x轴于C,交直线AB于点N,MD⊥y轴于D,NE⊥y轴于E,设四边形MDOC、NEOC的面积分别为S1、S2 , S=S2﹣S1 , 求S的最大值.
相关试题

