【题目】如图,已知反比例函数y= ![]() (x>0)的图象与一次函 数y=﹣x+b的图象分别交于A(1,3)、B两点.
(x>0)的图象与一次函 数y=﹣x+b的图象分别交于A(1,3)、B两点.
(1)求m、b的值;
(2)若点M是反比例函数图象上的一动点,直线MC⊥x轴于C,交直线AB于点N,MD⊥y轴于D,NE⊥y轴于E,设四边形MDOC、NEOC的面积分别为S1、S2 , S=S2﹣S1 , 求S的最大值.
参考答案:
【答案】
(1)解:把A(1,3)的坐标分别代入y= ![]() 、y=﹣x+b,
、y=﹣x+b,
∴m=xy=3,3=﹣1+b,
∴m=3,b=4
(2)解:由(1)知,反比例函数的解析式为y= ![]() ,一次函数的解析式为y=﹣x+4,
,一次函数的解析式为y=﹣x+4,
∵直线MC⊥x轴于C,交直线AB于点N,
∴可设点M的坐标为(x, ![]() ),点N的坐标为(x,﹣x+4),其中,x>0,
),点N的坐标为(x,﹣x+4),其中,x>0,
又∵MD⊥y轴于D,NE⊥y轴于E,∴四边形MDOC、NEOC都是矩形,
∴S1=x ![]() =3,S2=x(﹣x+4)=﹣x2+4x,
=3,S2=x(﹣x+4)=﹣x2+4x,
∴S=S2﹣S1=(﹣x2+4x)﹣3=﹣(x﹣2)2+1.其中,x>0,
∵a=﹣1<0,开口向下,
∴有最大值,
∴当x=2时,S取最大值,其最大值为1
【解析】(1)把A点的坐标代入反比例函数与一次函数的解析式,求出m,b即可;(2)设点M的坐标为(x, ![]() ),点N的坐标为(x,﹣x+4),求出四边形MDOC和MDEN的面积,代入求出S=(﹣x2+4x)﹣3,把上式化成顶点式,即可求出答案.
),点N的坐标为(x,﹣x+4),求出四边形MDOC和MDEN的面积,代入求出S=(﹣x2+4x)﹣3,把上式化成顶点式,即可求出答案.
【考点精析】本题主要考查了确定一次函数的表达式和比例系数k的几何意义的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小国同学的父亲参加旅游团到某地旅游,准备买某种礼物送给小国.据了解,沿旅游线路依次有A、B、C三个地点可以买到此种礼物,其质量相当,价格各不相同,但不知哪家更便宜.由于时间关系,随团旅游车不会掉头行驶.
(1)若到A处就购买,写出买到最低价格礼物的概率;
(2)小国同学的父亲认为,如果到A处不买,到B处发现比A处便宜就马上购买,否则到C处购买,这样更有希望买到最低价格的礼物.这个想法是否正确?试通过树状图分析说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】深化理解:
新定义:对非负实数x “四舍五入”到个位的值记为
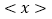 ,
,即:当n为非负整数时,如果
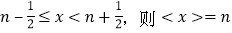 ;
;反之,当n为非负整数时,如果
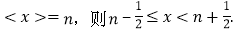
例如:<0> = <0.48> = 0,<0.64> = <1.49> = 1,<2> = 2,<3.5> = <4.12> = 4,……
试解决下列问题:
(1)填空:①
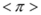 =________(
=________(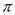 为圆周率); ②如果
为圆周率); ②如果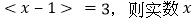 的取值范围为____________________.
的取值范围为____________________.(2)若关于x的不等式组
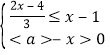 的整数解恰有3个,求a的取值范围.
的整数解恰有3个,求a的取值范围.(3)求满足
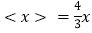 的所有非负实数x的值.
的所有非负实数x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C、D、E、F是⊙O的六等分点.
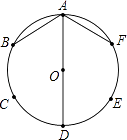
(1)连接AB、AD、AF,求证:AB+AF=AD;
(2)若P是圆周上异于已知六等分点的动点,连接PB、PD、PF,写出这三条线段长度的数量关系(不必说明理由). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB>BC,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于
 EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=
EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH= DH,③△ADH是等腰三角形,④S△ADH=
DH,③△ADH是等腰三角形,④S△ADH= S四边形ABCH.
S四边形ABCH.其中正确的有( )

A. ①②③ B. ①③④ C. ②④ D. ①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.
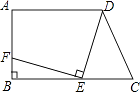
(1)若点F与B重合,求CE的长;
(2)若点F在线段AB上,且AF=CE,求CE的长;
(3)设CE=x,BF=y,写出y关于x的函数关系式(直接写出结果可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )
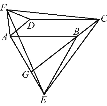
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
相关试题

