【题目】已知：∠AOB和两点C、D，求作一点P，使PC=PD，且点P到∠AOB的两边的距离相等．（要求：用尺规作图，保留作图痕迹，不写作法，不要求证明）

参考答案：

【答案】见详解.

【解析】

由所求的点P满足PC=PD，利用线段垂直平分线定理得到P点在线段CD的垂直平分线上，再由点P到∠AOB的两边的距离相等，利用角平分线定理得到P在∠AOB的角平分线上，故作出线段CD的垂直平分线，作出∠AOB的角平分线，两线交点即为所求的P点．

解：如图所示：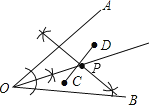

作法：（1）以O为圆心，任意长为半径画弧，与OA、OB分别交于两点；
（2）分别以这两交点为圆心，大于两交点距离的一半长为半径，在角内部画弧，两弧交于一点；
（3）以O为端点，过角内部的交点画一条射线；
（4）连接CD，分别为C、D为圆心，大于CD长为半径画弧，分别交于两点；
（5）过两交点画一条直线；
（6）此直线与前面画的射线交于点P，
∴点P为所求的点．

关闭