【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
参考答案:
【答案】(1)水果店两次分别购买了800元和1400元的水果.(2)该水果每千克售价至少为6元.
【解析】试题分析:(1)设该水果店两次分别购买了x元和y元的水果.根据“购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍”、“两次购进水果共花去了2200元”列出方程组并解答;
(2)设该水果每千克售价为a元,则由“售完这些水果获利不低于1244元”列出不等式并解答.
试题解析::(1)设该水果店两次分别购买了x元和y元的水果.根据题意,得
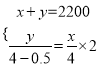 ,
,
解得![]() ,
,
经检验, ![]() 符合题意.
符合题意.
答:水果店两次分别购买了800元和1400元的水果.
(2)第一次所购该水果的重量为800÷4=200(千克).
第二次所购该水果的重量为200×2=400(千克).
设该水果每千克售价为a元,根据题意,得
[200(1-3%)+400(1-5%)]a-800-1400≥1244.
解得a≥6.
答:该水果每千克售价至少为6元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,点D,E分别在AC,BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB,BC分别交于点F,G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,
①求⊙E的半径;
②若Rt△ABC的内切圆圆心为I,则IE= .

-
科目: 来源: 题型:
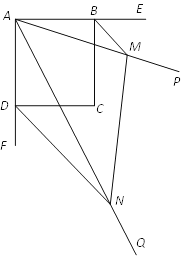
查看答案和解析>>【题目】已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一元二次方程x(x+5)=5x-10化成一般式的形式是( )
A. x2+10=0 B. x2-10=0 C. x2=-10 D. x2+50x+10=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】用总长为6米的铝合金做成一个如图所示的“日”字型窗框,设窗框的高度为x米,窗的透光面积(铝合金所占面积忽略不计)为y平方米.
(1)求y与x之间的函数关系式(结果要化成一般形式);
(2)能否使窗的透光面积达到2平方米,如果能,窗的高度和宽度各是多少?如果不能,试说明理由;
(3)窗的高度为多少时,能使透光面积最大?最大面积是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,⊙O是△ABC的内切圆,D、E、F是切点.

(1)求证:四边形ODCE是正方形;
(2)如果AC=6,BC=8,求内切圆⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,与y轴交于点C.
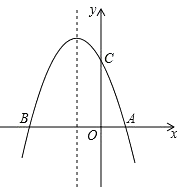
(1)求B、C两点的坐标;
(2)在该抛物线的对称轴上是否存在点P,使得△PAC的周长最小?若存在,求出点P的坐标;若不存在,请说明理由;
(3)抛物线在第二象限内是否存在一点Q,使△QBC的面积最大?,若存在,求出点Q的坐标及△QBC的面积最大值;若不存在,请说明理由.
相关试题

