搜索
【题目】观察下列图形：已知a∥b，在第一个图中，可得∠1+∠2=180°，则按照以上规律，∠1+∠2+∠P1+…+∠Pn=______度．
参考答案：
【答案】（n﹣1）×180
【解析】如图，
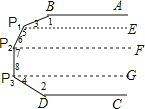
分别过P1、P2、P3作直线AB的平行线P1E，P2F，P3G，
∵AB∥CD，
∴AB∥P1E∥P2F∥P3G．
由平行线的性质可得出：∠1+∠3=180°，∠5+∠6=180°，∠7+∠8=180°，∠4+∠2=180°
∴（1）∠1+∠2=180°，
（2）∠1+∠P1+∠2=2×180，
（3）∠1+∠P1+∠P2+∠2=3×180°，
（4）∠1+∠P1+∠P2+∠P3+∠2=4×180°，
∴∠1+∠2+∠P1+…+∠Pn=（n+1）×180°．
故答案为：（n+1）×180．
-
科目： 来源： 题型：
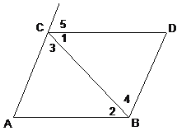
查看答案和解析>>【题目】如图,完成下列推理过程，已知AB∥CD,AC∥BD,
(1)∵AB∥CD（已知） ∴∠A＝∠5（两直线平行，_______________）；
(2)∵AC∥BD（已知） ∴∠3＝∠4（两直线平行，_______________）；
(3)∵AB∥CD（已知） ∴∠__＝∠___（两直线平行，內錯角相等）；
(4)∵AB∥CD（已知） ∴∠D +∠______ =180°(两直线平行，____)
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：
﹣ 
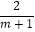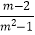÷（1﹣ 
）．其中m满足一元二次方程m2+（5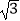 
tan30°）m﹣12cos60°=0． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB∥EF，则∠A、∠C、∠D、∠E满足的数量关系是（ ）
A. ∠A＋∠C＋∠D＋∠E＝360°
B. ∠A＋∠D＝∠C＋∠E
C. ∠A－∠C＋∠D＋∠E＝180°
D. ∠E－∠C＋∠D－∠A＝90°
-
科目： 来源： 题型：
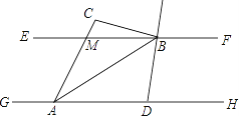
查看答案和解析>>【题目】如图，已知EF∥GH，A、D为GH上的两点，M、B为EF上的两点，延长AM于点C，AB平分∠DAC，直线DB平分∠FBC，若∠ACB=100°，则∠DBA的度数为________．
-
科目： 来源： 题型：
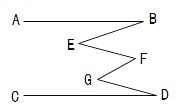
查看答案和解析>>【题目】如图，AB∥CD．证明：∠B+∠F+∠D=∠E+∠G．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在Rt△ABC中，∠ACB=90°，BD是△ABC的角平分线.
（1）如图1，若AD=BD，求∠A的度数；
（2）如图2，在（1）的条件下，作DE⊥AB于E，连接EC.求证：△EBC是等边三角形.
相关试题
