【题目】综合探究:如图1,在平面直角坐标系xOy中,抛物线y=﹣![]() +bx+8与x轴交于点A(﹣6,0)和点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE、EC.
+bx+8与x轴交于点A(﹣6,0)和点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE、EC.
(1)求抛物线的表达式及点C的坐标;
(2)连接AC交直线l于点D,则在点P运动过程中,当点D为EP中点时,S△ADP:S△CDE= ;
(3)如图2,当EC∥x轴时,点P停止运动,此时,在抛物线上是否存在点G,使得以点A、E、G为顶点的三角形是直角三角形?若存在,请求出点G的坐标,若不存在,说明理由.

参考答案:
【答案】(1)C(0,8)(2)1:2(3)存在点G使得以点A,E,G为顶点的三角形为直角三角形,符合条件的G点的坐标为G(![]() ,
, ![]() )或G(
)或G(![]() ,﹣
,﹣![]() ),
),
【解析】试题分析:(1)用待定系数法求出抛物线解析式,令![]() 求出
求出![]() 轴交点坐标;
轴交点坐标;
(2)先确定出直线![]() 解析式为
解析式为![]() 设出点E的坐标,表示出点
设出点E的坐标,表示出点![]() 而点D在直线AC上,列出方程
而点D在直线AC上,列出方程![]()
求出![]() ,从而得出结论;
,从而得出结论;
(3)先求出点![]() 的坐标,再分两种情况计算Ⅰ、当
的坐标,再分两种情况计算Ⅰ、当![]() 时,判断出△EMG∽△APE,得出比例式求解即可,Ⅱ、当
时,判断出△EMG∽△APE,得出比例式求解即可,Ⅱ、当![]() 时,判断出△GNA∽△APE,得到比例式计算.
时,判断出△GNA∽△APE,得到比例式计算.
试题解析:(1)∵点A(6,0)在抛物线![]() 上,
上,
∴![]()
![]()
∴![]()
令x=0,y=8,
∴C(0,8)
(2)设![]()
∴P(m,0),
∵点D为EP中点,
∴DP=DE, ![]()
∵A(6,0),C(0,8),
∴直线AC解析式为![]()
∵点D在直线AC上,
∴![]()
∴m=6(
∴P(4,0)
∴AP=2,OP=4,
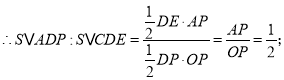
故答案为1:2
(3)存在点G使得以点A,E,G为顶点的三角形为直角三角形,
连接EG,AG,作GM⊥l,GN⊥x轴,
∵EC∥x轴,
∴EP=CO=8,
把y=8代入![]()
∴![]()
∴x=0(舍),或x=2,
∴P(2,0),
∴AP=AOPO=4,
Ⅰ、如图1,
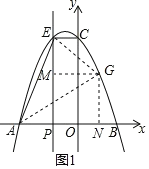
当![]() 时,
时,
∴![]()
∵![]()
∴∠MEG=∠EAP,
∵![]()
∴△EMG∽△APE,
∴![]()
设点![]()
![]()
∴![]()
MG=PN=PO+ON=2+m,
![]()
∴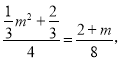 ∴m=2(舍)或
∴m=2(舍)或![]()
∴![]()
Ⅱ、如图2,
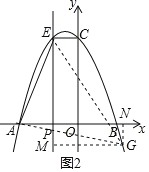
当![]() 时,
时,
∴![]()
∵![]()
∴∠NAG=∠AEP,
∵![]()
∴△GNA∽△APE,
∴![]()
设点![]()
![]()
∴AN=AO+ON=6+n,
∵![]()

∴n=6(舍),或![]()
∴![]()
符合条件的G点的坐标为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
如果一个三角形的三边长分别为a,b,c,记p=
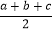 ,那么这个三角形的面积S=
,那么这个三角形的面积S=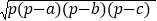 .这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:
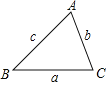
.这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:如图,在△ABC中,a=7,b=5,c=6.
(1)求△ABC的面积;
(2)设AB边上的高为h1,AC边上的高为h2,求h1 +h2的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)8+(-
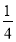 )-5-(-0.25); (2)|-
)-5-(-0.25); (2)|- |÷(
|÷( -
-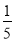 )×(-4)2.
)×(-4)2.(3)(
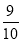 -
-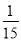 +
+ )×(-30); (4)(-1)3-(1-
)×(-30); (4)(-1)3-(1-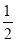 )÷3×[2-(-3)2].
)÷3×[2-(-3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上的A、B两点分别对应的数字为a、b,且a、b满足|4a-b|+(a-4)2=0.
(1)直接写出a、b的值;
(2)P从A出发,以每秒3个长度的速速延数轴正方向运动,当PA=PB时,求P运动的时间和P表示的数;
(3)数轴上还有一点C对应的数为36,若点P从A出发,以每秒3个单位的速度向C点运动,同时,Q从B点出发,以每秒1个长度的速度向正方向运动,点P运动到C点立立即返回再沿数轴向左运动.当PQ=10时,求P点对应的数.

-
科目: 来源: 题型:
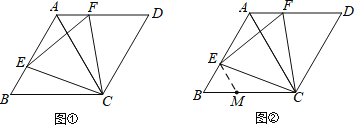
查看答案和解析>>【题目】如图,在菱形ABCD中,∠B= 60°.
(1)如图①.若点E、F分别在边AB、AD上,且BE=AF,求证:△CEF是等边三角形.
(2)小明发现,当点E、F分别在边AB、AD上,且∠CEF=60°时,△CEF也是等边三角形,
并通过画图验证了猜想;小丽通过探索,认为应该以CE= EF为突破口,构造两个全等三角形:小倩受到小丽的启发,尝试在BC上截取BM =BE,并连接ME,如图②,很快就证明了△CEF是等边三角形.请你根据小倩的方法,写出完整的证明过程.
相关试题

