【题目】如图,在菱形ABCD中,∠B= 60°.
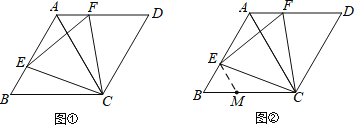
(1)如图①.若点E、F分别在边AB、AD上,且BE=AF,求证:△CEF是等边三角形.
(2)小明发现,当点E、F分别在边AB、AD上,且∠CEF=60°时,△CEF也是等边三角形,
并通过画图验证了猜想;小丽通过探索,认为应该以CE= EF为突破口,构造两个全等三角形:小倩受到小丽的启发,尝试在BC上截取BM =BE,并连接ME,如图②,很快就证明了△CEF是等边三角形.请你根据小倩的方法,写出完整的证明过程.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)易证△BEC≌△AFC,即可得证;(2)先证得△BEM是等边三角形,再证△MEC≌AFE,即可EC=EF,再由∠CEF=60°即可证明.
(1)因为四边形ABCD是菱形,所以AB= BC=CD=AD.
因为∠B=60°,所以△ABC,△ADC都是等边三角形.
所以BC=AC,∠B=∠CAF=∠ACB=60°,
又因为BE=AF,所以.△BEC≌△AFC(SAS),所以CE=CF,∠ECF=∠BCA=60°
所以△ECF是等边三角形,
(2) 因为BE=BM,∠B= 60°
所以△BEM是等边三角形.
所以∠EMB=∠BEM=60°,∠EMC=∠AEM=120°
因为AB= BC,∠EAF120°,所以.AE=CM,∠EAF=∠EM.
因为∠FEC=60°,所以∠AEF+∠CEM=60°.
又因为∠CEM+∠ECM=60°所以∠AEF=∠ECM.
所以△MEC≌AFE(ASA),所以EC=EF.
又因为∠FEC=60°,所以△EFC是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合探究:如图1,在平面直角坐标系xOy中,抛物线y=﹣
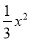 +bx+8与x轴交于点A(﹣6,0)和点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE、EC.
+bx+8与x轴交于点A(﹣6,0)和点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE、EC.(1)求抛物线的表达式及点C的坐标;
(2)连接AC交直线l于点D,则在点P运动过程中,当点D为EP中点时,S△ADP:S△CDE= ;
(3)如图2,当EC∥x轴时,点P停止运动,此时,在抛物线上是否存在点G,使得以点A、E、G为顶点的三角形是直角三角形?若存在,请求出点G的坐标,若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)8+(-
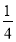 )-5-(-0.25); (2)|-
)-5-(-0.25); (2)|- |÷(
|÷( -
-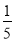 )×(-4)2.
)×(-4)2.(3)(
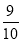 -
-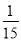 +
+ )×(-30); (4)(-1)3-(1-
)×(-30); (4)(-1)3-(1-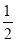 )÷3×[2-(-3)2].
)÷3×[2-(-3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上的A、B两点分别对应的数字为a、b,且a、b满足|4a-b|+(a-4)2=0.
(1)直接写出a、b的值;
(2)P从A出发,以每秒3个长度的速速延数轴正方向运动,当PA=PB时,求P运动的时间和P表示的数;
(3)数轴上还有一点C对应的数为36,若点P从A出发,以每秒3个单位的速度向C点运动,同时,Q从B点出发,以每秒1个长度的速度向正方向运动,点P运动到C点立立即返回再沿数轴向左运动.当PQ=10时,求P点对应的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从超市出发,向东走了3千米到达小彬家,继续向东走了1.5千米到达小颖家,然后向西走了9.5千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,请你在数轴上表示出小明家、小彬家和小颖家的位置.
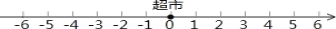
(2)小明家距小彬家多远?
(3)如果货车耗油量是每千米0.25升,那么在上述过程中共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表给出了1班6名学生的身高情况与全班平均身高的差值(单位:厘米)
学生
A
B
C
D
E
F
身高
157
162
159
152
163
164
身高与全班平均身高的差值
-3
+2
-1
a
+3
b
(1)列式计算表中数据a和b
(2)这6名学生的平均身高与全班学生的平均身高相比,在数值上有什么关系?(通过计算回答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如果大正方形的面积是13,小正方形的面积是4,直角三角形的较短直角边为a,较长直角边为b,那么
 的值为______________.
的值为______________.
相关试题

