搜索
【题目】计算：
(1)8＋(－
)－5－(－0.25)； (2)|－
|÷(
－
)×(－4)2．
(3)(
－
＋
)×(－30)； (4)(－1)3－(1－
)÷3×[2－(－3)2]．
参考答案：
【答案】（1）3(2) 
(3)-30 (4) 
.
【解析】
（1）根据有理数的加减运算法则即可求解；
（2）根据有理数的乘方及混合运算法则即可求解；
（3）根据乘法分配律即可求解；
（4）根据有理数的乘方及混合运算法则即可求解.
(1)8＋(－
)－5－(－0.25)；
=8-5-+0.25
=3
(2)|－
|÷(
－
)×(－4)2
=÷
×16
=×
×16
=
(3)(
－
＋)×(－30)
=-27+2-5
=-30；
(4)(－1)3－(1－
)÷3×[2－(－3)2]
=-1-×
×（-7）．
=-1+
=.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料:
如果一个三角形的三边长分别为a，b，c，记p=
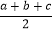，那么这个三角形的面积S=
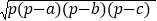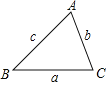
.这个公式叫“海伦公式”，它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式，称三斜求积术，故这个公式又被称为“海伦秦---九韶公式”完成下列问题:如图，在△ABC中，a=7，b=5，c=6.
（1）求△ABC的面积;
（2）设AB边上的高为h1，AC边上的高为h2，求h1 +h2的值
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合探究：如图1，在平面直角坐标系xOy中，抛物线y=﹣
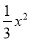+bx+8与x轴交于点A（﹣6，0）和点B（点A在点B左侧），与y轴交于点C，点P为线段AO上的一个动点，过点P作x轴的垂线l与抛物线交于点E，连接AE、EC．（1）求抛物线的表达式及点C的坐标；
（2）连接AC交直线l于点D，则在点P运动过程中，当点D为EP中点时，S△ADP：S△CDE= ；
（3）如图2，当EC∥x轴时，点P停止运动，此时，在抛物线上是否存在点G，使得以点A、E、G为顶点的三角形是直角三角形？若存在，请求出点G的坐标，若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上的A、B两点分别对应的数字为a、b，且a、b满足|4a－b|＋(a－4)2＝0．
(1)直接写出a、b的值；
(2)P从A出发，以每秒3个长度的速速延数轴正方向运动，当PA＝PB时，求P运动的时间和P表示的数；
(3)数轴上还有一点C对应的数为36，若点P从A出发，以每秒3个单位的速度向C点运动，同时，Q从B点出发，以每秒1个长度的速度向正方向运动，点P运动到C点立立即返回再沿数轴向左运动．当PQ＝10时，求P点对应的数．
-
科目： 来源： 题型：
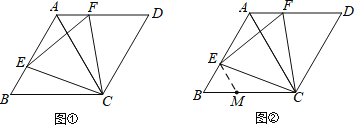
查看答案和解析>>【题目】如图，在菱形ABCD中，∠B= 60°.
（1）如图①.若点E、F分别在边AB、AD上，且BE=AF，求证:△CEF是等边三角形.
（2）小明发现，当点E、F分别在边AB、AD上，且∠CEF=60°时，△CEF也是等边三角形，
并通过画图验证了猜想;小丽通过探索，认为应该以CE= EF为突破口，构造两个全等三角形:小倩受到小丽的启发，尝试在BC上截取BM =BE，并连接ME，如图②，很快就证明了△CEF是等边三角形.请你根据小倩的方法，写出完整的证明过程.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一辆货车从超市出发，向东走了3千米到达小彬家，继续向东走了1.5千米到达小颖家，然后向西走了9.5千米到达小明家，最后回到超市.
(1)以超市为原点，以向东的方向为正方向，用1个单位长度表示1千米，请你在数轴上表示出小明家、小彬家和小颖家的位置.
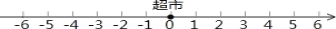
(2)小明家距小彬家多远?
(3)如果货车耗油量是每千米0.25升，那么在上述过程中共耗油多少升?
相关试题
