【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是( );
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示. 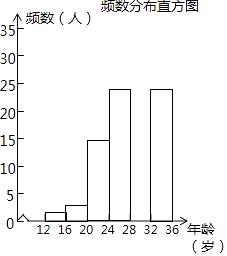
骑共享单车的人数统计表
年龄段(岁) | 频数 | 频率 |
12≤x<16 | 2 | 0.02 |
16≤x<20 | 3 | 0.03 |
20≤x<24 | 15 | a |
24≤x<28 | 25 | 0.25 |
28≤x<32 | b | 0.30 |
32≤x<36 | 25 | 0.25 |
根据以上信息解答下列问题:
①统计表中的a=;b=;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有人?
参考答案:
【答案】
(1)C
(2)0.15;30; 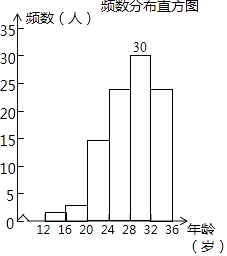 ;700
;700
【解析】解: (2)①a=15÷100=0.15,b=100×0.3=30,
③解:1000×(0.15+0.25+0.3)=700(人),
答:估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有700人.
所以答案是:0.15,30;700
【考点精析】认真审题,首先需要了解全面调查与抽样调查(全面调查收集到的数据全面、准确,但一般花费多、耗时长,而且某些调查不宜用全面调查;抽样调查具有花费少、省时的特点,但抽取的样本是否具有代表性,直接关系到对总体估计的准确程度),还要掌握频数分布直方图(特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图))的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=(m-3)x+5的函数值y随着x的增大而减小,则m的取值范围_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年冬奥会将在延庆召开,延庆区某中学响应区团委的号召,组织学生参加“我是奥运小志愿者”活动,志愿者可以到“八达岭长城”、“世葡园”、“龙庆峡”、“百里画廊”四个景区之一参加活动.晓明对“八达岭长城”和“百里画廊”最感兴趣,他将四个景区编号为A、B、C、D,并写在四张卡片上(除编号和内容不同之外,其余完全相同),他将卡片背面朝上,洗匀放好,从中随机抽取两张,请用列表或是画树状图的方法,求抽到的两张卡片恰好是“八达岭长城”,“百里画廊”的概率.(说明:这四张卡片分别用它的编号A、B、C、D表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=
 的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
(1)求m的值;
(2)若S△AOP=2S△AOB , 求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D是AB的中点,过点D作DE⊥AC于点E, 延长DE到点F,使得EF=DE,连接AF,CF.
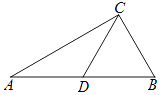
(1)根据题意,补全图形;
(2)求证:四边形ADCF是菱形;
(3)若AB=8,∠BAC=30°,求菱形ADCF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为__________个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若一组数据1、
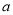 、2、3、4的平均数与中位数相同,则
、2、3、4的平均数与中位数相同,则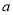 不可能是下列选项中的( )
不可能是下列选项中的( )A. 0 B. 2.5 C. 3 D. 5
相关试题

