【题目】某学校小组利用暑假中前40天参加社会实践活动,参与了一家网上书店经营,了解到一种成本每本20元的书在x天销售量P=50﹣x.在第x天的售价每本y元,y与x的关系如图所示. 已知当社会实践活动时间超过一半后.y=20+ ![]()

(1)请求出当1≤x≤20时,y与x的函数关系式,并求出第12天此书的销售单价;
(2)这40天中该网点销售此书第几天获得的利润最大?最大的利润是多少?
参考答案:
【答案】
(1)解:当1≤x≤20时,设y=kx+b,将(1,30.5),(20,40)代入得:
![]() ,
,
解得:  ,
,
则y与x的函数关系式为:y= ![]() x+30(1≤x≤20),
x+30(1≤x≤20),
当x=12时,y=6+30=36,
答:函数关系式为:y= ![]() x+30,第12天该商品的销售单价为每本36元
x+30,第12天该商品的销售单价为每本36元
(2)解:设该网店第x天获得的利润为w元.
当1≤x≤20时,w=( ![]() x+30﹣20)(50﹣x)=﹣
x+30﹣20)(50﹣x)=﹣ ![]() x2+15x+500=﹣
x2+15x+500=﹣ ![]() (x﹣15)2+
(x﹣15)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当x=15时,w有最大值w1,且w1= ![]() ,
,
当21≤x≤40时,w=(20+ ![]() ﹣20)(50﹣x)=
﹣20)(50﹣x)= ![]() ﹣315,
﹣315,
∵15750>0,
∴ ![]() 随x的增大而减小,
随x的增大而减小,
∴x=21时, ![]() 最大.
最大.
于是,x=21时,w有最大值w2,且w2= ![]() ﹣315=435,
﹣315=435,
∵w1>w2,
∴这40天中该网点销售此书第10天获得的利润最大,最大的利润是612.5元
【解析】(1)当1≤x≤20时,设y=kx+b,将(1,30.5),(20,40)代入,利用待定系数法求出y与x的函数关系式;然后在每个x的取值范围内,令y=35,分别解出x的值即可;(2)利用利润=售价﹣成本,分别求出在1≤x≤20和21≤x≤40时,获得的利润w与x的函数关系式;再利用二次函数及反比例函数的性质求出最大值,然后比较即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A (﹣4,2),B (﹣2,6),C (0,4)是直角坐标系平面上三点.

(1)把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1 , 画出平移后的图形;
(2)若△ABC内部有一点P (a,b),则平移后它的对应点Pl的坐标为;
(3)以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2 , 请在所给的坐标系中作出所有满足条件的图形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某书店老板去批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价20元出售,很快售完.由于该书畅销,第二次购书时,每本书批发价比第一次提高了25%,他用1800元所购该书数量比第一次多20本,又按定价售出全部图书.
(1)求该书原来每本的批发价;
(2)该老板这两次售书一共赚了多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次军事演习中,蓝方在﹣条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截.红方行驶2000米到达C后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同距离,刚好在D处成功拦截蓝方.
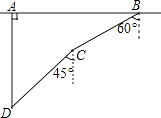
(1)求点C到公路的距离;
(2)求红蓝双方最初的距离.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC于D,若BD=AD,FD=CD.猜想:BF与AC的关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
相关试题

