Question

【题目】如图，一次军事演习中，蓝方在﹣条东西走向的公路上的A处朝正南方向撤退，红方在公路上的B处沿南偏西60°方向前进实施拦截．红方行驶2000米到达C后，因前方无法通行，红方决定调整方向，再朝南偏西45°方向前进了相同距离，刚好在D处成功拦截蓝方．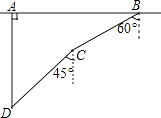

（1）求点C到公路的距离；
（2）求红蓝双方最初的距离．（结果保留根号）

Answer 1

【答案】
（1）

解：过B作AB的垂线，过C作AB的平行线，两线交于点E；过C作AB的垂线，过D作AB的平行线，两线交于点F，则∠E=∠F=90°，

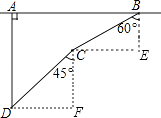
点C到公路的距离就是BE的长，

在Rt△BCE中，∵BC=2000米，∠EBC=60°，

∴BE=BCcos60°=2000× =1000米．

答：点C到公路的距离就是BE的长是1000米

（2）

解：红蓝双方相距AB=DF+CE．

在Rt△BCE中，

∵BC=2000米，∠EBC=60°，

∴CE=BCsin60°=2000× =1000 米．

在Rt△CDF中，

∵∠F=90°，CD=2000米，∠DCF=45°，

∴DF=CDsin45°=2000× =1000 米，

∴AB=DF+CE=（1000 +500 ）米．

答：红蓝双方最初相距（1000 +1000 ）米

【解析】过B作AB的垂线，过C作AB的平行线，两线交于点E；过C作AB的垂线，过D作AB的平行线，两线交于点F，则∠E=∠F=90°；（1）点C到公路的距离就是BE的长，在Rt△BCE中，根据三角函数可求BE的长．（2）红蓝双方相距AB=DF+CE．在Rt△BCE中，根据锐角三角函数的定义求出CE的长，同理，求出DF的长，进而可得出结论．
【考点精析】认真审题，首先需要了解关于方向角问题(指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角)．