【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)DE=BE-AD.
【解析】试题分析:(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,推出∠ACD=∠CBE,根据AAS可得Rt△ADC≌Rt△CEB,得到AD=CE,CD=BE,即可求出答案;
(2)与(1)证法类似可证出∠ACD=∠CBE,能推出△ADC≌△CEB,得到AD=CE,CD=BE,根据线段的和差即可得到答案;
(3)同前两问可得△ACD≌△CBE,得到AD=CE,CD=BE,根据线段的和差即可得出结论.
试题解析:
证明:(1)∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC与△CEB中,
∠ADC=∠CEB,∠ACD=∠CBE,AC=CB,
∴Rt△ADC≌Rt△CEB (AAS),
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;
(2)∵∠ACB=∠CEB=90°,
∴∠ACD+∠ECB=∠CBE+∠ECB=90°,
∴∠ACD=∠CBE
在△ADC与△CEB中,
∠ADC=∠CEB=90°,∠ACD=∠CBE,AC=CB,
∴△ADC≌△CEB (AAS),
∴AD=CE,DC=BE,
∴DE=CE-CD=AD-BE;
(3)DE=BE-AD.
理由:同(1)(2)证法可得△ADC≌△CEB ,
∴AD=CE,DC=BE,
∴DE=CD-CE=BE-AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】江津某服装店今年9月用4000元购进了一款秋衣若干件,上市后很快售完,服装店于10月初又购进同样数量的该款秋衣,由于第二批衬衣进货时价格比第一批衬衣进货时价格提高了20元,结果第二批衬衣进货用了5000元
(1)第一批秋衣进货时的价格是多少?
(2)第一批秋衣售价为120元/件,为保证第二批衬衣的利润率不低于第一批衬衣的利润率,那么第二批衬衣每件售价至少是多少元?
(提示:利润=售价﹣成本,利润率 =
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发, 匀速运动. 快车离乙地的路程y1(km) 与行驶的时间x(h) 之间的函数关系, 如图中线段AB 所示;慢车离乙地的路程y2(km) 与行驶的时间x(h)之间的函数关系, 如图中线段OC 所示。根据图象下列问题:
(1) 甲、乙两地之间的距离为__________km ;
(2) 线段AB 的解析式为_______________________;线段OC 的解析式为_________________________;
(3) 设快、慢车之间的距离为y(km), 求y 与慢车行驶时间x(h) 的函数关系式, 并画出函数的图象。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,
 ).
).(1)求∠BAO的度数;
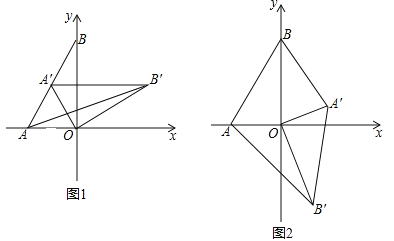
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
相关试题

