搜索
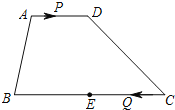
【题目】如图，在梯形ABCD中，AD∥BC，AD=6，BC=16，E是BC的中点．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿CB向点B运动．点P停止运动时，点Q也随之停止运动．
（1）当运动时间t为多少秒时，PQ∥CD．
（2）当运动时间t为多少秒时，以点P，Q，E，D为顶点的四边形是平行四边形．
参考答案：
【答案】（1）当运动时间t为1.5秒时，PQ∥CD；（2）当运动时间t为1或3.5秒时，以点P，Q，E，D为顶点的四边形是平行四边形．
【解析】
根据题意得：AP=t，CQ=3t，（1）根据平行四边形性质得6-t=3t；（2）①当Q运动到E和B之间，设运动时间为t，则得：3t-8=6-t；②当Q运动到E和C之间，设运动时间为t，则得：8-3t=6-t.
根据题意得：AP=t，CQ=3t，
∵AD=6，BC=16，
∴PD=AD-AP=6-t；
（1）∵AD∥BC，
∴当PD=CQ时，四边形CDPQ是平行四边形，此时PQ∥CD，
∴6-t=3t，
解得：t=1.5；
∴当运动时间t为1.5秒时，PQ∥CD．
（2）∵E是BC的中点，
∴BE=CE=
BC=8，
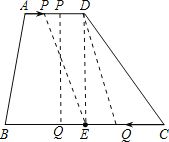
①当Q运动到E和B之间，设运动时间为t，则得：
3t-8=6-t，
解得：t=3.5；
②当Q运动到E和C之间，设运动时间为t，则得：
8-3t=6-t，
解得：t=1，
∴当运动时间t为1或3.5秒时，以点P，Q，E，D为顶点的四边形是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市正在开展“食品安全城市”创建活动，为了解学生对食品安全知识的了解情况，学校随机抽取了部分学生进行问卷调查，将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计，并绘制了下列两幅统计图（不完整）．请根据图中信息，解答下列问题：
（1）此次共调查了 名学生；
（2）扇形统计图中D所在扇形的圆心角为 ；
（3）将上面的条形统计图补充完整；
（4）若该校共有800名学生，请你估计对食品安全知识“非常了解”的学生的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：对于给定的两个函数，任取自变量x的一个值，当x<0时，它们对应的函数值互为相反数：当x≥0时，它们对应的函数值相等，我们把这样的两个函数称作互为友好函数，例如：一次函数y=x-2，它的友好函数为y=
（1）直接写出一次函数y=-2x+1的友好函数．
（2）已知点A(2，5)在一次函数y=ax-1的友好函数的图象上，求a的值.
（3）已知点B(m，
)在一次函数y= 
x-1的友好函数的图象上，求m的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】在“端午”期间，小明、小亮等同学随家长一同到某公园游玩，下面是购买门票时，小明与他爸爸的对话(如图)，试根据图中的信息，解答下列问题：
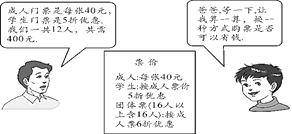
(1)他们共去了几个成人，几个学生？
(2)请你帮助算算，小明用更省钱的购票方式是指什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，对于任意两点A（x1，y1）B （x2，y2），规定运算：
（1）A⊕B=（x1+x2，y1+y2）；
（2）A⊙B=x1x2+y1y2；
（3）当x1=x2且y1=y2时，A=B．
有下列四个命题：
①若有A（1，2），B（2，﹣1），则A⊕B=（3，1），A⊙B=0；
②若有A⊕B=B⊕C，则A=C；
③若有A⊙B=B⊙C，则A=C；
④（A⊕B）⊕C=A⊕（B⊕C）对任意点A、B、C均成立．
其中正确的命题为______（只填序号）
-
科目： 来源： 题型：
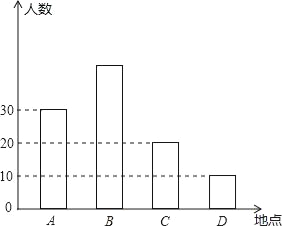
查看答案和解析>>【题目】如图，暑假快要到了，某市准备组织同学们分别到A，B，C，D四个地方进行夏令营活动，前往四个地方的人数．
（1）去B地参加夏令营活动人数占总人数的40%，根据统计图求去B地的人数？
（2）若一对姐弟中只能有一人参加夏令营，姐弟俩提议让父亲决定．父亲说：现有4张卡片上分别写有1，2，3，4四个整数，先让姐姐随机地抽取一张后放回，再由弟弟随机地抽取一张．若抽取的两张卡片上的数字之和是5的倍数则姐姐参加，若抽取的两张卡片上的数字之和是3的倍数则弟弟参加．用列表法或树形图分析这种方法对姐弟俩是否公平？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角
和坝底宽AD.（结果保留根号）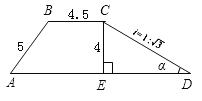
相关试题
