【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

参考答案:
【答案】(1)AE+CF=EF,证明见解析;(2)![]() ,理由见解析.
,理由见解析.
【解析】
(1)由题干中截长补短的提示,再结合第(1)问的证明结论,在第二问可以用截长补短的方法来构造全等,从而达到证明结果.
(2)同理作辅助线,同理进行即可,直接写出猜想,并证明.
(1)图2猜想:AE+CF=EF,
证明:在BC的延长线上截取CA'=AE,连接A'D,

∵∠DAB=∠BCD=90°,
∴∠DAB=∠DCA'=90°,
又∵AD=CD,AE=A'C,
∴△DAE≌△DCA'(SAS),
∴ED=A'D,∠ADE=∠A'DC,
∵∠ADC=120°,
∴∠EDA'=120°,
∵∠EDF=60°,
∴∠EDF=∠A'DF=60°,
又DF=DF,
∴△EDF≌△A'DF(SAS),
则EF=A'F=FC+CA'=FC+AE;
(2)如图3,AE+CF=EF,

证明:在BC的延长线上截取CA'=AE,连接A'D,
∵∠DAB与∠BCD互补,∠BCD+∠DCA'=180°
∴∠DAB=∠DCA',
又∵AD=CD,AE=A'C,
∴△DAE≌△DCA'(SAS),
∴ED=A'D,∠ADE=∠A'DC,
∵∠ADC=2α,
∴∠EDA'=2α,
∵∠EDF=α,
∴∠EDF=∠A'DF=α
又DF=DF,
∴△EDF≌△A'DF(SAS),
则EF=A'F=FC+CA'=FC+AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
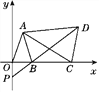
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
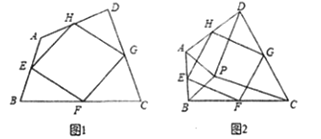
(1)如图1,四边形
 中,点
中,点 ,
,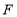 ,
,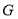 ,
,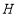 分别为边
分别为边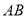 、
、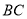 、
、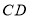 、
、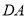 的中点,则中点四边形
的中点,则中点四边形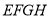 形状是_______________.
形状是_______________.(2)如图2,点
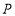 是四边形
是四边形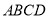 内一点,且满足
内一点,且满足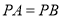 ,
,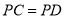 ,
,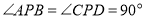 ,点
,点 ,
, ,
, ,
,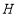 分别为边
分别为边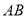 、
、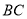 、
、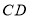 、
、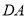 的中点,求证:中点四边形
的中点,求证:中点四边形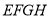 是正方形.
是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校共有1000名学生,为了了解他们的视力情况,随机抽查了部分学生的视力,并将调查的数据整理绘制成直方图和扇形图.

(1)这次共调查了多少名学生?扇形图中的
 、
、 值分别是多少?
值分别是多少?(2)补全频数分布直方图;
(3)在光线较暗的环境下学习的学生占对应被调查学生的比例如下表:
视力

0.35~0.65
0.65~0.95
0.95~1.25
1.25~l.55
比例





根据调查结果估计该校有多少学生在光线较暗的环境下学习?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴交于A(3,0),B两点,与y轴交于点C,点M(
与x轴交于A(3,0),B两点,与y轴交于点C,点M( ,5)是抛物线
,5)是抛物线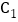 上一点,抛物线
上一点,抛物线 与抛物线
与抛物线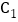 关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′
关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′(1)求抛物线C1的解析式;
(2)过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D. P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】生活中,有人喜欢把传送的便条折成“
 ”形状,折叠过程按图
”形状,折叠过程按图 的顺序进行(其中阴影部分表示纸条的反面):
的顺序进行(其中阴影部分表示纸条的反面): 
如果由信纸折成的长方形纸条(图①)长
 厘米,分别回答下列问题:
厘米,分别回答下列问题:(1)如图①、图②,如果长方形纸条的宽为
 厘米,并且开始折叠时
厘米,并且开始折叠时 厘米,那么在图②中,
厘米,那么在图②中, ____厘米.
____厘米.(2)如图②,如果长方形纸条的宽为
 厘米,现在不但要折成图②的形状,还希望纸条两端超出点
厘米,现在不但要折成图②的形状,还希望纸条两端超出点 的部分
的部分 和
和 相等,使图②. 是轴对称图形,
相等,使图②. 是轴对称图形, ______厘米.
______厘米.(3)如图④,如果长方形纸条的宽为
 厘米,希望纸条两端超出点
厘米,希望纸条两端超出点 的部分
的部分 和
和 相等,即最终图形是轴对称图形,试求在开始折叠时起点
相等,即最终图形是轴对称图形,试求在开始折叠时起点 与点
与点 的距离(结果用
的距离(结果用 表示) .
表示) . -
科目: 来源: 题型:
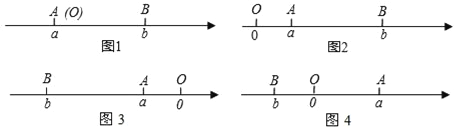
查看答案和解析>>【题目】阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
相关试题

