【题目】某校共有1000名学生,为了了解他们的视力情况,随机抽查了部分学生的视力,并将调查的数据整理绘制成直方图和扇形图.

(1)这次共调查了多少名学生?扇形图中的![]() 、
、![]() 值分别是多少?
值分别是多少?
(2)补全频数分布直方图;
(3)在光线较暗的环境下学习的学生占对应被调查学生的比例如下表:
视力 |
| 0.35~0.65 | 0.65~0.95 | 0.95~1.25 | 1.25~l.55 |
比例 |
|
|
|
|
|
根据调查结果估计该校有多少学生在光线较暗的环境下学习?
参考答案:
【答案】(1)200名,a=18%,b=20%;(2)见解析;(3)270名
【解析】
(1)根据第四组的频数与其所占的百分比求出被调查的学生数.
(2)根据各组所占的百分比分别计算他们的频数,从而补全频数分布直方图.
(3)首先计算各组在光线较暗的环境下学习的学生数,再根据被抽取的学生数所占的比例进行估算该校有多少学生在光线较暗的环境下学习.
(1)这次共调查的学生为:![]() (名).
(名).
![]() .
.![]() .
.
(2)0.35~0.65的频数为:![]() ;0.95~1.25的频数为:
;0.95~1.25的频数为:![]() .
.
补全频数分布直方图如下:

(3)各组在光线较暗的环境下学习的学生总数为:
![]() (名).
(名).
该校学生在光线较暗的环境下学习的有:![]() (名).
(名).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数阵是由50个偶数排成的.
(1)在数阵中任意做一类似于图中的框,设其中最小的数为x,那么其他3个数怎样表示?
(2)如果这四个数的和是172,能否求出这四个数?
(3)如果扩充数阵的数据,框中的四个数的和可以是2019吗?为什么?

-
科目: 来源: 题型:
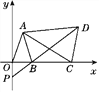
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
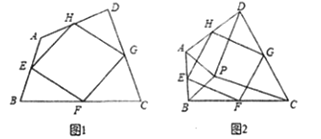
(1)如图1,四边形
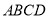 中,点
中,点 ,
,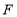 ,
,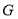 ,
,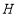 分别为边
分别为边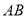 、
、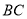 、
、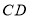 、
、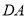 的中点,则中点四边形
的中点,则中点四边形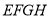 形状是_______________.
形状是_______________.(2)如图2,点
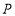 是四边形
是四边形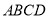 内一点,且满足
内一点,且满足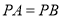 ,
,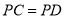 ,
,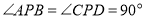 ,点
,点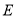 ,
,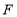 ,
,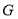 ,
,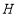 分别为边
分别为边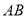 、
、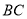 、
、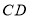 、
、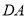 的中点,求证:中点四边形
的中点,求证:中点四边形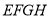 是正方形.
是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴交于A(3,0),B两点,与y轴交于点C,点M(
与x轴交于A(3,0),B两点,与y轴交于点C,点M( ,5)是抛物线
,5)是抛物线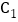 上一点,抛物线
上一点,抛物线 与抛物线
与抛物线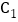 关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′
关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′(1)求抛物线C1的解析式;
(2)过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D. P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】生活中,有人喜欢把传送的便条折成“
 ”形状,折叠过程按图
”形状,折叠过程按图 的顺序进行(其中阴影部分表示纸条的反面):
的顺序进行(其中阴影部分表示纸条的反面): 
如果由信纸折成的长方形纸条(图①)长
 厘米,分别回答下列问题:
厘米,分别回答下列问题:(1)如图①、图②,如果长方形纸条的宽为
 厘米,并且开始折叠时
厘米,并且开始折叠时 厘米,那么在图②中,
厘米,那么在图②中, ____厘米.
____厘米.(2)如图②,如果长方形纸条的宽为
 厘米,现在不但要折成图②的形状,还希望纸条两端超出点
厘米,现在不但要折成图②的形状,还希望纸条两端超出点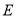 的部分
的部分 和
和 相等,使图②. 是轴对称图形,
相等,使图②. 是轴对称图形, ______厘米.
______厘米.(3)如图④,如果长方形纸条的宽为
 厘米,希望纸条两端超出点
厘米,希望纸条两端超出点 的部分
的部分 和
和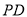 相等,即最终图形是轴对称图形,试求在开始折叠时起点
相等,即最终图形是轴对称图形,试求在开始折叠时起点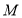 与点
与点 的距离(结果用
的距离(结果用 表示) .
表示) .
相关试题

