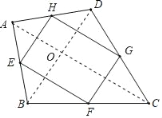
【题目】如图,在四边形ABCD中,AB=AD,BC=CD,E,F,G,H分别为AB,BC,CD,AD的中点,顺次连接E,G,F,H,求证:四边形EFGH是矩形.

参考答案:
【答案】见解析.
【解析】
根据连接AC、BD交于点O,根据三角形中位线定理、平行四边形的判定定理得到四边形EFGH是平行四边形,再根据线段垂直平分线的性质、矩形的判定定理证明.
连接AC、BD交于点O,
∵E,F分别为AB,BC的中点,
∴EF∥AC,EF=![]() AC,
AC,
∵G,H分别为CD,AD的中点,
∴HG∥AC,HG=![]() AC,
AC,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形,
∵AB=AD,BC=CD,
∴AC是线段BD的垂直平分线,
∵E,H分别为AB,AD的中点,
∴EH∥BD,又EF∥AC,
∴∠HEF=90°,
∴四边形EFGH是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:
x
…
﹣1
0
1
2
3
4
5
…
y1
…
0
﹣3
﹣4
﹣3
0
5
12
…
y2
…
0
2
4
6
8
10
12
…
请你根据表格信息回答下列问题,
(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为;
(2)当y1>y2时,自变量x的取值范围是;
(3)请写出二次函数y1=ax2+bx+c的三条不同的性质. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料解决问题
两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,例如37和82,它们各数位上的数字之和分别为3+7和8+2,显然3+7=8+2=10故37和82互为“调和数”.
(1)下列说法错误的是
A.123和51互为调和数” B.345和513互为“调和数
C.2018和8120互为“调和数” D.两位数
 和
和 互为“调和数”
互为“调和数”(2)若A、B是两个不等的两位数,A=
 ,B=
,B= ,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A.
,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年5月,某城遭遇暴雨水灾,武警战士乘一冲锋舟从A地逆流而上,前往C地营救受困群众,途经B地时,由所携带的救生艇将B地受困群众运回A地,冲锋舟继续前进,到C地接到群众后立刻返回A地,途中曾与救生艇相遇,冲锋舟和救生艇距A地的距离y(千米)和冲锋舟出发后所用时间x(分)之间的函数图象如图所示,假设群众上下冲锋舟和救生艇的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(1)冲锋舟从A地到C地的时间为 分钟,冲锋舟在静水中的速度为 千米/分,水流的速度为 千米/分.
(2)冲锋舟将C地群众安全送到A地后,又立即去接应救生艇,已知救生艇与A地的距离y(千米)和冲锋舟出发后所用时间x(分钟)之间的函数关系式为y=kx+b,若冲锋舟在距离A地
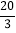 千米处与救生艇第二次相遇,求k、b的值.
千米处与救生艇第二次相遇,求k、b的值.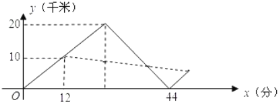
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM.

(1)求证:AM与⊙O相切;
(2)若AM=3DM,BC=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家禽养殖场,用总长为110m的围栏靠墙(墙长为22m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,设AD长为xm,矩形区域ABCD的面积为ym2 .
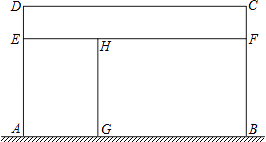
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
相关试题

