【题目】观察下列等式:![]() ,
,![]() ,
,![]() ,则以上三个等式两边分别相加得:
,则以上三个等式两边分别相加得:![]() .
.
![]() 观察发现
观察发现
![]() ______;
______;![]() ______.
______.
![]() 拓展应用
拓展应用
有一个圆,第一次用一条直径将圆周分成两个半圆![]() 如图
如图![]() ,在每个分点标上质数m,记2个数的和为
,在每个分点标上质数m,记2个数的和为![]() ;第二次再将两个半圆周都分成
;第二次再将两个半圆周都分成![]() 圆周
圆周![]() 如图
如图![]() ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的![]() ,记4个数的和为
,记4个数的和为![]() ;第三次将四个
;第三次将四个![]() 圆周分成
圆周分成![]() 圆周
圆周![]() 如图
如图![]() ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的![]() ,记8个数的和为
,记8个数的和为![]() ;第四次将八个
;第四次将八个![]() 圆周分成
圆周分成![]() 圆周,在新产生的分点标上相邻的已标的两个数的和的
圆周,在新产生的分点标上相邻的已标的两个数的和的![]() ,记16个数的和为
,记16个数的和为![]() ;
;![]() 如此进行了n次.
如此进行了n次.
![]() ______
______![]() 用含m、n的代数式表示
用含m、n的代数式表示![]() ;
;
![]() 当
当![]() 时,求
时,求![]() 的值.
的值.

参考答案:
【答案】(1)![]() ,
,![]() (2)①
(2)①![]() ②
②![]()
【解析】
![]() 观察发现:先根据题中所给出的列子进行猜想,写出猜想结果即可;根据第一空中的猜想计算出结果;
观察发现:先根据题中所给出的列子进行猜想,写出猜想结果即可;根据第一空中的猜想计算出结果;
![]() 由
由![]() ,
,![]() ,
,![]() ,
,![]() ,找规律可得结论;
,找规律可得结论;
![]() 由
由![]() 知
知![]() ,据此可得
,据此可得![]() ,
,![]() ,再进一步求解可得.
,再进一步求解可得.
![]() 观察发现:
观察发现:
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
故答案为:![]() ,
,![]() .
.
![]() 拓展应用
拓展应用
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
故答案为:![]()
![]() ,且m为质数,
,且m为质数,
对6188分解质因数可知![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要设计一个等腰梯形的花坛,花坛上底120米,下底180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.

(1)用含x的式子表示横向甬道的面积;
(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元? -
科目: 来源: 题型:
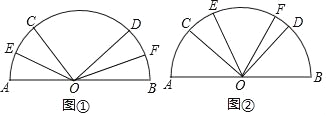
查看答案和解析>>【题目】点C,D是半圆弧上的两个动点,在运动的过程中保持∠COD=100°.
(1)如图①,OE平分∠AOC,OF平分∠BOD,求∠EOF的度数;
(2)如图②,已知∠AOC的度数为x,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
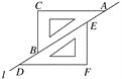
A. BD=AE
B. CB=BF
C. BE⊥CF
D. BA平分∠CBF
-
科目: 来源: 题型:
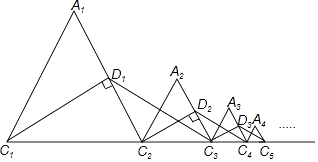
查看答案和解析>>【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1 , 在C1C2的延长线上取点C3 , 使D1C3=D1C1 , 连接D1C3 , 以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2 , 在C2C3的延长线上取点C4 , 使D2C4=D2C2 , 连接D2C4 , 以C3C4为边作等边△A3C3C4;…且点A1 , A2 , A3 , …都在直线C1C2同侧,如此下去,则△A1C1C2 , △A2C2C3 , △A3C3C4 , …,△AnCnCn+1的周长和为 . (n≥2,且n为整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D,F分别在AB,AC边上,此时BD=CF,BD⊥CF成立.
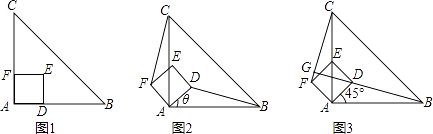
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.求证:BD⊥CF;
(3)在(2)小题的条件下,AC与BG的交点为M,当AB=4,AD=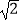 时,求线段CM的长.
时,求线段CM的长.
相关试题

