【题目】如图,要设计一个等腰梯形的花坛,花坛上底120米,下底180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.
(1)用含x的式子表示横向甬道的面积;
(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
参考答案:
【答案】
(1)解:横向甬道的面积为: ![]() x=150x(m2)
x=150x(m2)
(2)解:横向甬道的面积为: ![]() x=150x(m2);
x=150x(m2);
甬道总面积为150x+160x﹣2x2=310x﹣2x2,
依题意:310x﹣2x2= ![]() ×
× ![]() ×80,
×80,
整理得:x2﹣155x+750=0,
x1=5,x2=150(不符合题意,舍去),
∴甬道的宽为5米;
(3)解:∵花坛上底120米,下底180米,上下底相距80米,
∴等腰梯形的面积为: ![]() (120+180)×80=12000,
(120+180)×80=12000,
∵甬道总面积为S=310x﹣2x2,
绿化总面积为12000﹣S,
花坛总费用y=甬道总费用+绿化总费用:
∴y=5.7x+(12000﹣S)×0.02,
=5.7x﹣0.02S+240,
=5.7x﹣0.02(310x﹣2x2)+240,
=0.04x2﹣0.5x+240,
当x=﹣ ![]() =6.25时,y的值最小.
=6.25时,y的值最小.
∵根据设计的要求,甬道的宽不能超过6米,
∴当x=6米时,总费用最少.
即最少费用为:0.04×62﹣3+240=238.44万元.
【解析】(1)先求出横向甬道的长即梯形的中位线长,即可求出其面积。
(2)根据题意先求出甬道总面积,再根据甬道总面积=![]()
![]() 梯形面积。建立方程求解即可。
梯形面积。建立方程求解即可。
(3)分别求出等腰梯形的面积、甬道总面积、绿化总面积,再根据花坛总费用y=甬道总费用+绿化总费用,建立函数关系式,再求出顶点坐标,根据设计要求甬道的宽不能超过6米,求出当x=6时的函数值即可。
【考点精析】认真审题,首先需要了解二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a),还要掌握梯形的中位线(梯形的中位线平行于梯形的两底并等于两底和的一半)的相关知识才是答题的关键.
-
科目: 来源: 题型:
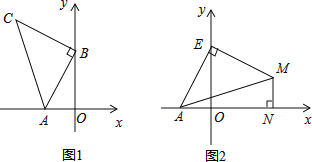
查看答案和解析>>【题目】如图1,
 ,
, ,以B点为直角顶点在第二象限作等腰直角
,以B点为直角顶点在第二象限作等腰直角 .
.
 求C点的坐标;
求C点的坐标; 在坐标平面内是否存在一点P,使
在坐标平面内是否存在一点P,使 与
与 全等?若存在,直接写出P点坐标,若不存在,请说明理由;
全等?若存在,直接写出P点坐标,若不存在,请说明理由; 如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角
如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角 ,过M作
,过M作 轴于N,直接写出
轴于N,直接写出 的值为 .
的值为 . -
科目: 来源: 题型:
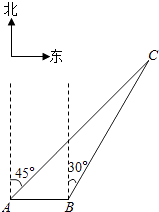
查看答案和解析>>【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况如图所示:根据条形图提供的信息,下列说法中,正确的是( )
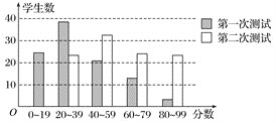
A. 两次测试,最低分在第二次测试中
B. 第一次测试和第二次测试的平均分相同
C. 第一次分数的中位数在20~39分数段
D. 第二次分数的中位数在60~79分数段
-
科目: 来源: 题型:
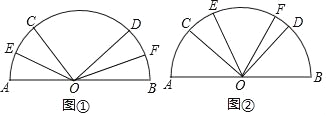
查看答案和解析>>【题目】点C,D是半圆弧上的两个动点,在运动的过程中保持∠COD=100°.
(1)如图①,OE平分∠AOC,OF平分∠BOD,求∠EOF的度数;
(2)如图②,已知∠AOC的度数为x,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
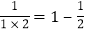 ,
,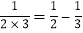 ,
,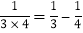 ,则以上三个等式两边分别相加得:
,则以上三个等式两边分别相加得: .
. 观察发现
观察发现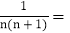 ______;
______;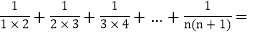 ______.
______.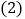 拓展应用
拓展应用有一个圆,第一次用一条直径将圆周分成两个半圆
 如图
如图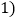 ,在每个分点标上质数m,记2个数的和为
,在每个分点标上质数m,记2个数的和为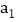 ;第二次再将两个半圆周都分成
;第二次再将两个半圆周都分成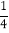 圆周
圆周 如图
如图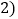 ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的 ,记4个数的和为
,记4个数的和为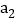 ;第三次将四个
;第三次将四个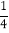 圆周分成
圆周分成 圆周
圆周 如图
如图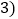 ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的 ,记8个数的和为
,记8个数的和为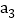 ;第四次将八个
;第四次将八个 圆周分成
圆周分成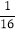 圆周,在新产生的分点标上相邻的已标的两个数的和的
圆周,在新产生的分点标上相邻的已标的两个数的和的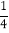 ,记16个数的和为
,记16个数的和为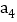 ;
; 如此进行了n次.
如此进行了n次. ______
______ 用含m、n的代数式表示
用含m、n的代数式表示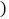 ;
; 当
当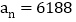 时,求
时,求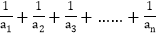 的值.
的值.
相关试题

