【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.

参考答案:
【答案】(1)详见解析;(2)①详见解析;②:ME=BD,证明详见解析;③∠CNE的度数为7.5°、15°、82.5°、150°.
【解析】
(1)根据中垂线的判定定理“与一条线段两个端点距离相等的点,在这条线段的垂直平分线上”可得出结论.
(2)①由∠CAD=15°,BD=AD与直角等腰三角形的性质可知,∠DBA=∠DAB=30°,则可得∠BDE=30°+30°=60°,又根据SSS可证△ADC≌△BDC,则∠ACD=∠BCD=45°,可知∠CDE=∠ACD+∠CAD=45°+15°=60°,故DE平分∠BDC.
②连接MC,由DC=DM,∠CDE=60°,可知△MCD为等边三角形,∠ECM=∠CMD-∠CAD=45°则根据SAS可证△BDC≌△EMC,得出结论ME=BD.
③根据题意可知,分类:当EN=EC时;当EN=CN时;当CE=CN时三种情况求出∠CNE的度数.
(1)证明:∵CB=CA,DB=DA,
∴CD垂直平分线段AB,
∴CD⊥AB,
故答案为:CD⊥AB.
(2)①证明:∵AC=BC,
∴∠CBA=∠CAB,
又∵∠ACB=90°,
∴∠CBA=∠CAB=45°,
又∵在△ADC和△BDC中,
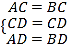 ,
,
∴△ADC≌△BDC(SSS),
∴∠CAD=∠CBD=15°,
∴∠DBA=∠DAB=30°,
∴∠BDE=30°+30°=60°,
∵∠ACB=90°,∠ACD=∠BCD,
∴∠ACD=∠BCD=45°,
∴∠CDE=∠ACD+∠CAD=45°+15°=60°,
∵∠CDE=∠BDE=60°,
∴DE平分∠BDC;
故答案为:DE平分∠BDC.
②结论:ME=BD,
理由:连接MC,

∵DC=DM,∠CDE=60°,
∴△MCD为等边三角形,
∴CM=CD,∠CMD=60°,
又∵EC=CA,∠CAD=15°,
∴∠ECM=∠CMD-∠CAD=45°,
在△BDC和△EMC中,
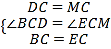 ,
,
∴△BDC≌△EMC(SAS),
∴ME=BD,
故答案为:ME=BD.
③当EN=EC时,∠ENC=7.5°或82.5°;
当EN=CN时,∠ENC=150°;
当CE=CN时,∠CNE=15°,
故答案为:∠CNE的度数为7.5°、15°、82.5°、150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况如图所示:根据条形图提供的信息,下列说法中,正确的是( )
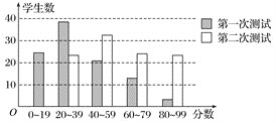
A. 两次测试,最低分在第二次测试中
B. 第一次测试和第二次测试的平均分相同
C. 第一次分数的中位数在20~39分数段
D. 第二次分数的中位数在60~79分数段
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要设计一个等腰梯形的花坛,花坛上底120米,下底180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.

(1)用含x的式子表示横向甬道的面积;
(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元? -
科目: 来源: 题型:
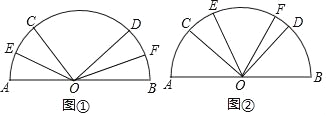
查看答案和解析>>【题目】点C,D是半圆弧上的两个动点,在运动的过程中保持∠COD=100°.
(1)如图①,OE平分∠AOC,OF平分∠BOD,求∠EOF的度数;
(2)如图②,已知∠AOC的度数为x,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
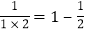 ,
,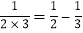 ,
,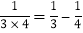 ,则以上三个等式两边分别相加得:
,则以上三个等式两边分别相加得: .
.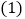 观察发现
观察发现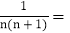 ______;
______;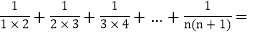 ______.
______.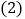 拓展应用
拓展应用有一个圆,第一次用一条直径将圆周分成两个半圆
 如图
如图 ,在每个分点标上质数m,记2个数的和为
,在每个分点标上质数m,记2个数的和为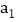 ;第二次再将两个半圆周都分成
;第二次再将两个半圆周都分成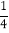 圆周
圆周 如图
如图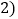 ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的 ,记4个数的和为
,记4个数的和为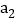 ;第三次将四个
;第三次将四个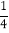 圆周分成
圆周分成 圆周
圆周 如图
如图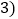 ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的 ,记8个数的和为
,记8个数的和为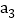 ;第四次将八个
;第四次将八个 圆周分成
圆周分成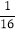 圆周,在新产生的分点标上相邻的已标的两个数的和的
圆周,在新产生的分点标上相邻的已标的两个数的和的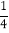 ,记16个数的和为
,记16个数的和为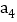 ;
; 如此进行了n次.
如此进行了n次. ______
______ 用含m、n的代数式表示
用含m、n的代数式表示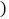 ;
; 当
当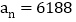 时,求
时,求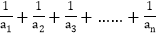 的值.
的值.
-
科目: 来源: 题型:
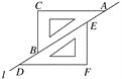
查看答案和解析>>【题目】如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
A. BD=AE
B. CB=BF
C. BE⊥CF
D. BA平分∠CBF
-
科目: 来源: 题型:
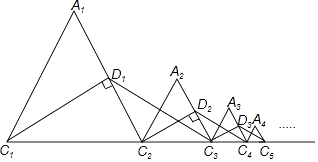
查看答案和解析>>【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1 , 在C1C2的延长线上取点C3 , 使D1C3=D1C1 , 连接D1C3 , 以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2 , 在C2C3的延长线上取点C4 , 使D2C4=D2C2 , 连接D2C4 , 以C3C4为边作等边△A3C3C4;…且点A1 , A2 , A3 , …都在直线C1C2同侧,如此下去,则△A1C1C2 , △A2C2C3 , △A3C3C4 , …,△AnCnCn+1的周长和为 . (n≥2,且n为整数)
相关试题

