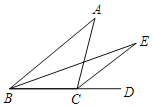
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1 , 在C1C2的延长线上取点C3 , 使D1C3=D1C1 , 连接D1C3 , 以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2 , 在C2C3的延长线上取点C4 , 使D2C4=D2C2 , 连接D2C4 , 以C3C4为边作等边△A3C3C4;…且点A1 , A2 , A3 , …都在直线C1C2同侧,如此下去,则△A1C1C2 , △A2C2C3 , △A3C3C4 , …,△AnCnCn+1的周长和为 . (n≥2,且n为整数)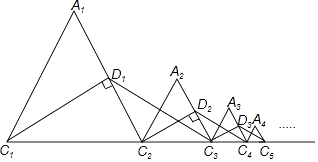
参考答案:
【答案】![]()
【解析】∵等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,
∴A1D1=D1C2,
∴△A2C2C3的周长= ![]() △A1C1C2的周长=
△A1C1C2的周长= ![]() ,
,
∴△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长分别为1, ![]() ,
, ![]() ,…,
,…, ![]() ,
,
∴△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长和为1+ ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
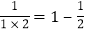 ,
,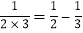 ,
,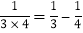 ,则以上三个等式两边分别相加得:
,则以上三个等式两边分别相加得: .
.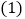 观察发现
观察发现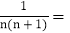 ______;
______;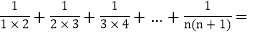 ______.
______.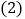 拓展应用
拓展应用有一个圆,第一次用一条直径将圆周分成两个半圆
 如图
如图 ,在每个分点标上质数m,记2个数的和为
,在每个分点标上质数m,记2个数的和为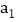 ;第二次再将两个半圆周都分成
;第二次再将两个半圆周都分成 圆周
圆周 如图
如图 ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的 ,记4个数的和为
,记4个数的和为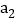 ;第三次将四个
;第三次将四个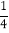 圆周分成
圆周分成 圆周
圆周 如图
如图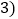 ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的 ,记8个数的和为
,记8个数的和为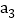 ;第四次将八个
;第四次将八个 圆周分成
圆周分成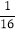 圆周,在新产生的分点标上相邻的已标的两个数的和的
圆周,在新产生的分点标上相邻的已标的两个数的和的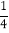 ,记16个数的和为
,记16个数的和为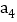 ;
; 如此进行了n次.
如此进行了n次. ______
______ 用含m、n的代数式表示
用含m、n的代数式表示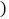 ;
; 当
当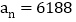 时,求
时,求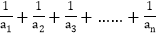 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
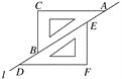
A. BD=AE
B. CB=BF
C. BE⊥CF
D. BA平分∠CBF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D,F分别在AB,AC边上,此时BD=CF,BD⊥CF成立.
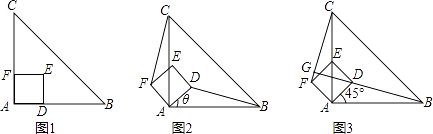
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.求证:BD⊥CF;
(3)在(2)小题的条件下,AC与BG的交点为M,当AB=4,AD=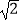 时,求线段CM的长.
时,求线段CM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板如图1摆放在直线MN上,在三角板OAB和三角板OCD中,
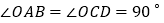 ,
,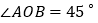 ,
,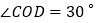 .
.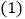 保持三角板OCD不动,将三角板OAB绕点O以每秒
保持三角板OCD不动,将三角板OAB绕点O以每秒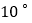 的速度逆时针旋转,旋转时间为t秒.
的速度逆时针旋转,旋转时间为t秒. 当
当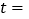 ______秒时,OB平分
______秒时,OB平分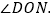 此时
此时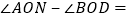 ______
______ ;
; 当三角板OAB旋转至图2的位置,此时
当三角板OAB旋转至图2的位置,此时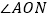 与
与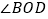 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由;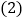 如图3,若在三角板OAB开始旋转的同时,另一个三角板OCD也绕点O以每秒
如图3,若在三角板OAB开始旋转的同时,另一个三角板OCD也绕点O以每秒 的速度逆时针旋转,当OB旋转至射线OM上时同时停止.
的速度逆时针旋转,当OB旋转至射线OM上时同时停止. 当t为何值时,OB平分
当t为何值时,OB平分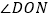 ?
? 直接写出在旋转过程中,
直接写出在旋转过程中,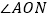 与
与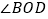 之间的数量关系.
之间的数量关系.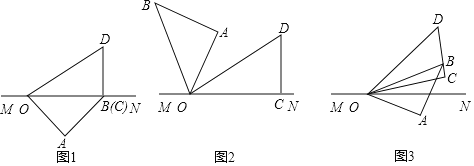
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=40°,∠ACD=76°, BE平分∠ABC,CE平分△ABC的外角∠ACD,则∠E=( ).
A. 20°B. 36°C. 38°D. 18°
相关试题

