【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D,F分别在AB,AC边上,此时BD=CF,BD⊥CF成立.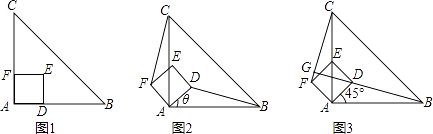
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.求证:BD⊥CF;
(3)在(2)小题的条件下,AC与BG的交点为M,当AB=4,AD= ![]() 时,求线段CM的长.
时,求线段CM的长.
参考答案:
【答案】
(1)解:BD=CF成立.
理由:∵△ABC是等腰直角三角形,四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∵∠BAD=∠BAC﹣∠DAC,∠CAF=∠DAF﹣∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,
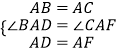 ,
,
∴△BAD≌△CAF(SAS),
∴BD=CF.
(2)证明:设BG交AC于点M,
∵△BAD≌△CAF,
∴∠ABM=∠GCM,
∵∠BMA=∠CMG,
∴△BMA∽△CMG,
∴∠BGC=∠BAC=90°,
∴BD⊥CF.
(3)解:过点F作FN⊥AC于点N,
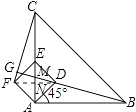
∵在正方形ADEF中,AD=DE= ![]() ,
,
∴AE= ![]() =2,
=2,
∴AN=FN= ![]() AE=1.
AE=1.
∵在等腰直角△ABC中,AB=AC=4,
∴CN=AC﹣AN=3,BC= ![]() =4
=4 ![]() ,
,
∴在Rt△FCN中,tan∠FCN= ![]() =
= ![]() ,
,
∴在Rt△ABM中,tan∠ABM= ![]() =tan∠FCN=
=tan∠FCN= ![]() ,
,
∴AM= ![]() AB=
AB= ![]() ,
,
∴CM=AC﹣AM=4﹣ ![]() =
= ![]()
【解析】(1)根据△ABC是等腰直角三角形,四边形ADEF是正方形,根据角边角关系证出△BAD≌△CAF,根据全等三角形的对应边相等,即可证得BD=CF。
(2)先设BG交AC于点M,根据(1)证出的△BAD≌△CAF,可得∠ABM=∠GCM,又根据对顶角相等,得出△BMA∽△CMG,再根据根据相似三角形的对应角相等,可得∠BGC=∠BAC=90°,即可证出BD⊥CF。
(3)首先过点F作FN⊥AC于点N,利用勾股定理即可求得AE,BC的长,继而求得AN,CN的长,又由等角的三角函数值相等,可求得AM的值,从而求出CM的值。
【考点精析】本题主要考查了等腰三角形的性质和正方形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
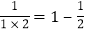 ,
,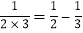 ,
,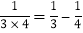 ,则以上三个等式两边分别相加得:
,则以上三个等式两边分别相加得: .
.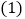 观察发现
观察发现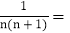 ______;
______;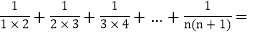 ______.
______.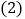 拓展应用
拓展应用有一个圆,第一次用一条直径将圆周分成两个半圆
 如图
如图 ,在每个分点标上质数m,记2个数的和为
,在每个分点标上质数m,记2个数的和为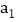 ;第二次再将两个半圆周都分成
;第二次再将两个半圆周都分成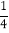 圆周
圆周 如图
如图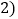 ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的 ,记4个数的和为
,记4个数的和为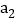 ;第三次将四个
;第三次将四个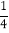 圆周分成
圆周分成 圆周
圆周 如图
如图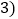 ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的 ,记8个数的和为
,记8个数的和为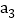 ;第四次将八个
;第四次将八个 圆周分成
圆周分成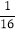 圆周,在新产生的分点标上相邻的已标的两个数的和的
圆周,在新产生的分点标上相邻的已标的两个数的和的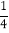 ,记16个数的和为
,记16个数的和为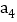 ;
; 如此进行了n次.
如此进行了n次. ______
______ 用含m、n的代数式表示
用含m、n的代数式表示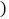 ;
; 当
当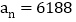 时,求
时,求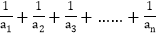 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
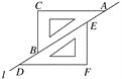
A. BD=AE
B. CB=BF
C. BE⊥CF
D. BA平分∠CBF
-
科目: 来源: 题型:
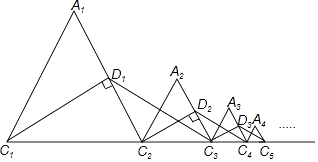
查看答案和解析>>【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1 , 在C1C2的延长线上取点C3 , 使D1C3=D1C1 , 连接D1C3 , 以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2 , 在C2C3的延长线上取点C4 , 使D2C4=D2C2 , 连接D2C4 , 以C3C4为边作等边△A3C3C4;…且点A1 , A2 , A3 , …都在直线C1C2同侧,如此下去,则△A1C1C2 , △A2C2C3 , △A3C3C4 , …,△AnCnCn+1的周长和为 . (n≥2,且n为整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板如图1摆放在直线MN上,在三角板OAB和三角板OCD中,
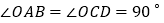 ,
,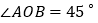 ,
,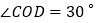 .
.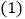 保持三角板OCD不动,将三角板OAB绕点O以每秒
保持三角板OCD不动,将三角板OAB绕点O以每秒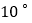 的速度逆时针旋转,旋转时间为t秒.
的速度逆时针旋转,旋转时间为t秒. 当
当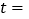 ______秒时,OB平分
______秒时,OB平分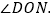 此时
此时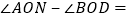 ______
______ ;
; 当三角板OAB旋转至图2的位置,此时
当三角板OAB旋转至图2的位置,此时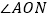 与
与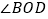 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由; 如图3,若在三角板OAB开始旋转的同时,另一个三角板OCD也绕点O以每秒
如图3,若在三角板OAB开始旋转的同时,另一个三角板OCD也绕点O以每秒 的速度逆时针旋转,当OB旋转至射线OM上时同时停止.
的速度逆时针旋转,当OB旋转至射线OM上时同时停止. 当t为何值时,OB平分
当t为何值时,OB平分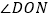 ?
? 直接写出在旋转过程中,
直接写出在旋转过程中,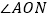 与
与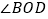 之间的数量关系.
之间的数量关系.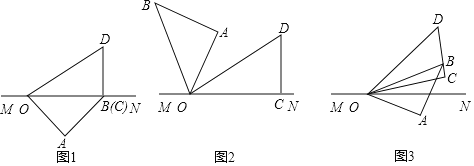
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=40°,∠ACD=76°, BE平分∠ABC,CE平分△ABC的外角∠ACD,则∠E=( ).
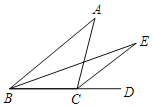
A. 20°B. 36°C. 38°D. 18°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形有( )

A. 1对
B. 2对
C. 3对
D. 4对
相关试题

