【题目】定义:有一组邻边相等的凸四边形叫做“准菱形”.利用该定义完成以下各题:
(1) 理解
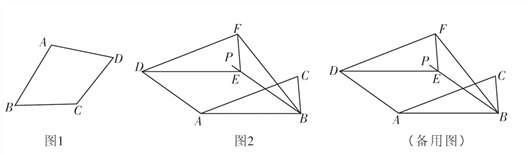
填空:如图1,在四边形ABCD中,若 (填一种情况),则四边形ABCD是“准菱形”;
(2)应用
证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,求证并证明)
(3) 拓展
如图2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF,连接AD,BF,若平移后的四边形ABFD是“准菱形”,求线段BE的长.
参考答案:
【答案】(1)答案不唯一,如AB=BC.(2)见解析;(3) BE=2或![]() 或
或![]() 或
或![]() .
.
【解析】整体分析:
(1)根据“准菱形”的定义解答,答案不唯一;(2)对角线相等且互相平分的四边形是矩形,矩形的邻边相等时即是正方形;(3)根据平移的性质和“准菱形”的定义,分四种情况画出图形,结合勾股定理求解.
解:(1)答案不唯一,如AB=BC.
(2)已知:四边形ABCD是“准菱形”,AB=BC,对角线AC,BO交于点O,且AC=BD,OA=OC,OB=OD.
求证:四边形ABCD是正方形.
证明:∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
∵AC=BD,
∴平行四边形ABCD是矩形.
∵四边形ABCD是“准菱形”,AB=BC,
∴四边形ABCD是正方形.
(3)由平移得BE=AD,DE=AB=2,EF=BC=1,DF=AC=![]() .
.
由“准菱形”的定义有四种情况:
①如图1,当AD=AB时,BE=AD=AB=2.
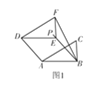
②如图2,当AD=DF时,BE=AD=DF=![]() .
.
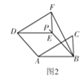
③如图3,当BF=DF=![]() 时,延长FE交AB于点H,则FH⊥AB.
时,延长FE交AB于点H,则FH⊥AB.
∵BE平分∠ABC,∴∠ABE=![]() ∠ABC=45°.
∠ABC=45°.
∴∠BEH=∠ABE=45°.∴BE=![]() BH.
BH.
设EH=BH=x,则FH=x+1,BE=![]() x.
x.
∵在Rt△BFH中,BH2+FH2=BF2,
∴x2+(x+1)2=(![]() )2,
)2,
解得x1=1,x2=-2(不合题意,舍去),
∴BE=![]() x=
x=![]() .
.
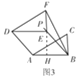
④如图4,当BF=AB=2时,与③)同理得:BH2+FH2=BF2.
设EH=BH=x,则x2+(x+1)2=22,
解得x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
∴BE=![]() x=
x=![]() .
.
综上所述,BE=2或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天昆明市交警大队的一辆警车在东西方向的街上巡视,警车从钟楼A处出发,规定向东方向为正,当天行驶纪录如下(单位:千米)
+10,-9,+7,-15,+6,-5,+4,-2
(1)最后警车是否回到钟楼A处?若没有,在钟楼A处何方,距钟楼A多远?
(2)警车行驶1千米耗油0.2升,油箱有油10升,够不够?若不够,途中还需补充多少升油?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
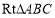 中,
中,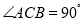 ,过点
,过点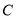 的直线
的直线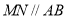 ,
, 为
为 边上一点,过点
边上一点,过点 作
作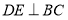 ,交直线
,交直线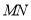 于点
于点 ,垂足为
,垂足为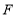 ,连接
,连接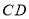 ,
, .
.(1)求证:
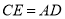 ;
;(2)当
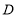 为
为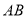 的中点时,四边形
的中点时,四边形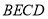 是什么特殊四边形?请说明你的理由;
是什么特殊四边形?请说明你的理由;(3)若
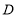 为
为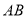 的中点,则当
的中点,则当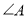 的大小满足什么条件时,四边形
的大小满足什么条件时,四边形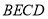 是正方形?请说明你的理由.
是正方形?请说明你的理由.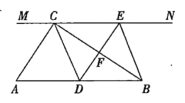
-
科目: 来源: 题型:
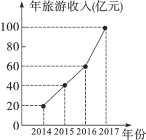
查看答案和解析>>【题目】某人为了解他所在地区的旅游情况,收集了该地区2014年到2017年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题:
(1)该地区2014年到2017年四年的年旅游平均收入是多少亿元;
(2)从折线统计图中你能获得哪些信息?
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形各个内角的平分线围成一个四边形,则这个四边形一定是( )
A. 正方形 B. 菱形 C. 矩形 D. 平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接期末考试,某中学对全校七年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图两幅不完整的统计图,请根据图中所给出的信息,解答下列问题:
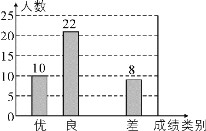

(1)在这次调查中,被抽取的学生的总人数为多少?
(2)请将表示成绩类别为“中”的条形统计图补充完整.
(3)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角的度数是多少?
(4)学校七年级共有1000人参加了这次数学考试,估计该校七年级共有多少名学生的数学成绩可以达到优秀.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1 ,一次函数
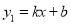 (k,b为常数,k≠0)的图象与反比例函数
(k,b为常数,k≠0)的图象与反比例函数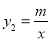 (m为常数,m≠0)的图象相交于点M(1,4)和点N(4,n).
(m为常数,m≠0)的图象相交于点M(1,4)和点N(4,n).(1)填空:①反比例函数的解析式是 ; ②根据图象写出
 时自变量x的取值范围是 ;
时自变量x的取值范围是 ;(2) 若将直线MN向下平移a(a>0)个单位长度后与反比例函数的图象有且只有一个公共点,求a的值;
(3) 如图2,函数
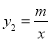 的图象(x>0)上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交
的图象(x>0)上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交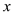 轴于点A,交
轴于点A,交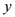 轴点B,若BC=2CA, 求OA·OB的值.
轴点B,若BC=2CA, 求OA·OB的值.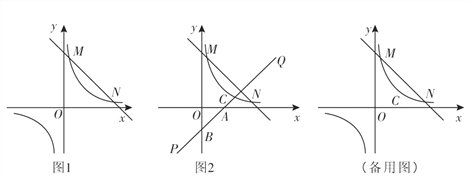

相关试题

