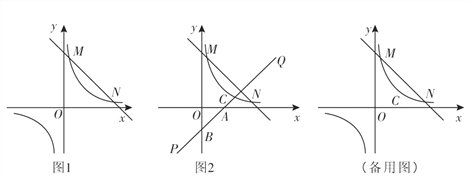
【题目】如图1 ,一次函数![]() (k,b为常数,k≠0)的图象与反比例函数
(k,b为常数,k≠0)的图象与反比例函数![]() (m为常数,m≠0)的图象相交于点M(1,4)和点N(4,n).
(m为常数,m≠0)的图象相交于点M(1,4)和点N(4,n).
(1)填空:①反比例函数的解析式是 ; ②根据图象写出![]() 时自变量x的取值范围是 ;
时自变量x的取值范围是 ;
(2) 若将直线MN向下平移a(a>0)个单位长度后与反比例函数的图象有且只有一个公共点,求a的值;
(3) 如图2,函数![]() 的图象(x>0)上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交
的图象(x>0)上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交![]() 轴于点A,交
轴于点A,交![]() 轴点B,若BC=2CA, 求OA·OB的值.
轴点B,若BC=2CA, 求OA·OB的值.
![]()
参考答案:
【答案】(1) ① y=![]() .②
.②![]() ;(2) a=1或a=9.;(3) 18或2..
;(2) a=1或a=9.;(3) 18或2..
【解析】整体分析:
(1)由点A的坐标求反比例函数的解析式,得到点B的坐标; ![]() ,即是一次函数的图象在反比例函数图象的下方时自变量的范围;(2)由点M,N的坐标求直线MN的解析式,直线MN向下平移a(a>0)个单位长度后与反比例函数的图象有且只有一个公共点,即是方程kx+b-a=
,即是一次函数的图象在反比例函数图象的下方时自变量的范围;(2)由点M,N的坐标求直线MN的解析式,直线MN向下平移a(a>0)个单位长度后与反比例函数的图象有且只有一个公共点,即是方程kx+b-a=![]() 的判别式等于0;(3)设点C(a,b),根据BC=2CA,分三种情况讨论,利用△ACH∽△ABO,结合ab=4求解.
的判别式等于0;(3)设点C(a,b),根据BC=2CA,分三种情况讨论,利用△ACH∽△ABO,结合ab=4求解.
解:(1)k=1×4=4,所以y=![]() .
.
②当y=4时,x=![]() ,则B(4,1).
,则B(4,1).
根据图象得: ![]() .
.
(2)点M(1,4)和点N(4,1)分别代入![]() 得
得![]()
直线AB向下平移a个单位长度后的解析式为y=-x+5-a,
把y=![]() 代入消去y,整理,得x2-(5-a)x+4=0.
代入消去y,整理,得x2-(5-a)x+4=0.
∵平移后的直线与反比例函数的图象有且只有一个公共点,
∴Δ=(5-a)2-16=0.
解得a=1或a=9.
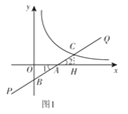
(3)设点C(a,b),则ab=4如图1,过C点作CH⊥OA于点H.
①当点B在y轴的负半轴时,如图1
∵BC=2CA,∴AB=CA.
∵∠AOB=∠AHC=90°,∠1=∠2,
∴△ACH∽△ABO.
∴OB=CH=b,OA=AH=0.5a
∴![]() .
.
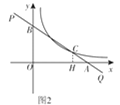
②当点B在y轴的正半轴时,
如图2,当点A在x轴的正半轴时,
∵BC=2CA,∴. ![]()
∵CH∥OB,∴△ACH∽△ABO.
∴![]()
∴.OB=3b,OA=1.5a
∴![]() .
.
如图3,当点A在x轴的负半轴时,BC=2CA不可能.
综上所述,OA·OB的值为18或2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一组邻边相等的凸四边形叫做“准菱形”.利用该定义完成以下各题:
(1) 理解
填空:如图1,在四边形ABCD中,若 (填一种情况),则四边形ABCD是“准菱形”;
(2)应用
证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,求证并证明)
(3) 拓展
如图2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF,连接AD,BF,若平移后的四边形ABFD是“准菱形”,求线段BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形各个内角的平分线围成一个四边形,则这个四边形一定是( )
A. 正方形 B. 菱形 C. 矩形 D. 平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接期末考试,某中学对全校七年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图两幅不完整的统计图,请根据图中所给出的信息,解答下列问题:
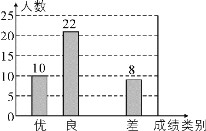

(1)在这次调查中,被抽取的学生的总人数为多少?
(2)请将表示成绩类别为“中”的条形统计图补充完整.
(3)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角的度数是多少?
(4)学校七年级共有1000人参加了这次数学考试,估计该校七年级共有多少名学生的数学成绩可以达到优秀.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB
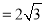 ,BC
,BC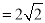 ,连结对角线AC,点O为AC的中点,点E为线段BC上的一个动点,连结OE,将△AOE沿OE翻折得到△FOE,EF与AC交于点G,若△EOG的面积等于△ACE的面积的
,连结对角线AC,点O为AC的中点,点E为线段BC上的一个动点,连结OE,将△AOE沿OE翻折得到△FOE,EF与AC交于点G,若△EOG的面积等于△ACE的面积的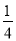 ,则BE=_____.
,则BE=_____.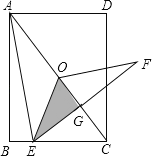
-
科目: 来源: 题型:
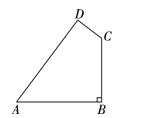
查看答案和解析>>【题目】如图,某开发区有一块四边形空地ABCD,现计划在空地上种植草皮,经测量,∠B=90°,AB=20m,BC=15m,CD=7m,AD=24m.若每平方米草皮需要200元,则种植这片草皮需要多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为t.

(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
相关试题

