【题目】在平面直角坐标系xOy中,点A(0,4),B(3,0),以AB为边在第一象限内作正方形ABCD,直线L:y=kx+3.
(1)当直线l经过D点时,求点D的坐标及k的值;
(2)当直线L与正方形有两个交点时,直接写出k的取值范围.
参考答案:
【答案】(1)D(4,7),k=1;(2)k>﹣1
【解析】试题分析:(1)过D点作DE⊥y轴,证△AED≌△BOA,根据全等求出DE=AO=4,AE=OB=3,即可得出D的坐标,把D的坐标代入解析式即可求出k的值;
(2)把B的坐标代入求出K的值,即可得出答案.
试题解析:解:(1)如图,过D点作DE⊥y轴,
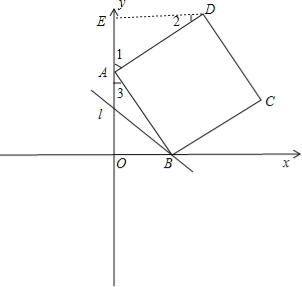
则∠AED=∠1+∠2=90°.
在正方形ABCD中,∠DAB=90°,AD=AB.
∴∠1+∠3=90°,
∴∠2=∠3.
又∵∠AOB=∠AED=90°,
在△AED和△BOA中,
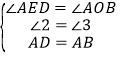 ,
,
∴△AED≌△BOA,
∴DE=AO=4,AE=OB=3,
∴OE=7,
∴D点坐标为(4,7),
把D(4,7)代入y=kx+3,得k=1;
(2)当直线y=kx+3过B点时,把(3,0)代入得:0=3k+3,
解得:k=﹣1.
所以当直线l与正方形有两个交点时,k的取值范围是k>﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点P(-3,4)先向下平移3个单位,再向右平移2个单位后得到点Q,则点Q的坐标是______.
-
科目: 来源: 题型:
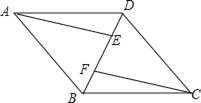
查看答案和解析>>【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连结EM并延长交线段CD的延长线于点F.
(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作MG⊥EF交线段BC于点G,求证:△GEF是等腰直角三角形;
(3)如图3,若AB=2
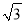 ,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.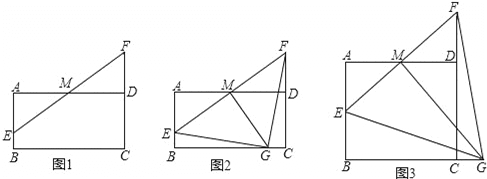
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.
(1)求该抛物线的解析式及点D的坐标;
(2)连接AC,CD,BD,BC,设△AOC、△BOC、△BCD的面积分别为S1,S2和S3,求证:S3=
 ;
;(3)点M是线段AB上一动点(不包括点A和点B),过点M作MN∥BC交AC于点N,连接MC,是否存在点M使∠AMN=∠ACM?若存在,求出点M的坐标和此时直线MN的解析式;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】运用等式性质进行的变形,不正确的是( )
A.如果a=b,那么a﹣c=b﹣c
B.如果a=b,那么a+c=b+c
C.如果a=b,那么ac=bc
D.如果ac=bc,那么a=b -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABF中,C为AF上一点且AB=AC.
(1)尺规作图:作出以AB为直径的⊙O,⊙O分别交AC、BC于点D、E,在图上标出D、E,在图上标出D、E(保留作图痕迹,不写作法).
(2)若∠BAF=2∠CBF,求证:直线BF是⊙O的切线;
(3)在(2)中,若AB=5,sin∠CBF=
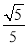 ,求BC和BF的长.
,求BC和BF的长.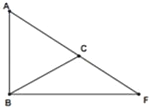
相关试题

