【题目】已知二次函数y=ax2-8ax(a<0)的图像与x轴的正半轴交于点A,它的顶点为P.点C为y轴正半轴上一点,直线AC与该图像的另一交点为B,与过点P且垂直于x轴的直线交于点D,且CB:AB=1:7.
(1)求点A的坐标及点C的坐标(用含a的代数式表示);
(2)连接BP,若△BDP与△AOC相似(点O为原点),求此二次函数的关系式.

参考答案:
【答案】(1)A(8,0), C(0,-8a).(2) ![]()
【解析】试题分析:(1)由y=ax2-8ax可得A(8,0),由CB:AB=1:7得点B的横坐标为1,故B(1,-7a),C(0,-8a).
(2)对称轴与x轴交于点H,过点B作BF⊥PD于点F,易知,BF=3,AH=4,DH=-4a,则FD=-3a, PF=-9a,由相似,可知:BF2=DF·PF,从而求得a的值,故可求函数关系式.
试题解析:(1)P(4,-16a),A(8,0),
∵CB:AB=1:7,
∴点B的横坐标为1
∴B(1,-7a),
∴C(0,-8a).
(2)∵△AOC为直角三角形,
∴只可能∠PBD=90°,且△AOC∽△PBD.………(5分)
设对称轴与x轴交于点H,过点B作BF⊥PD于点F,
易知,BF=3,AH=4,DH=-4a,则FD=-3a,
∴PF=-9a,
由相似,可知:BF2=DF·PF,
∴9=-9a·(-3a),
∴a=![]() , a=-
, a=-![]() (舍去).
(舍去).
∴y=-![]() x2-
x2-![]() x.
x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a3(3an-2am+4ak)=3a9-2a6+4a4,则m,n,k的值分别为( )
A. 6,3,1 B. 3,6,1 C. 2,1,3 D. 2,3,1
-
科目: 来源: 题型:
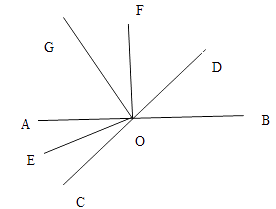
查看答案和解析>>【题目】如图,AB与CD相交于O , OE平分∠AOC , OF⊥AB于O , OG⊥OE于O , 若∠BOD=40°,求∠AOE和∠FOG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),点P是等腰三角形ABC底边BC上的一动点,过点P作BC的垂线,交直线AB于点Q,交CA的延长线于点R.
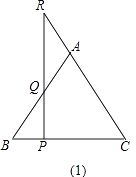
(1)请观察AR与AQ,它们相等吗?并证明你的猜想.
(2)如图(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图(2)中完成图形,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中,正确的是( )
A.若5x﹣6=7,则5x=7﹣6
B.若﹣3x=5,则x=﹣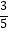
C.若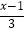 +
+ 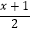 =1,则2(x﹣1)+3(x+1)=1
=1,则2(x﹣1)+3(x+1)=1
D.若﹣ x=1,则x=﹣3
x=1,则x=﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
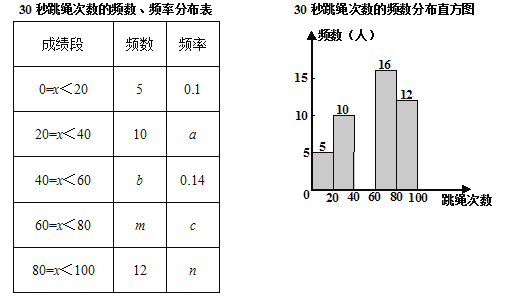
根据以上图表信息,解答下列问题:
(1)表中的a= ,m= ;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?
-
科目: 来源: 题型:
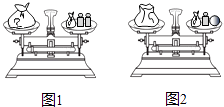
查看答案和解析>>【题目】如图1,天平呈平衡状态,其中左侧秤盘中有一袋玻璃球,右侧秤盘中也有一袋玻璃球,还有2个各20克的砝码.现将左侧袋中一颗玻璃球移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图2,则被移动的玻璃球的质量为( )
A.10克
B.15克
C.20克
D.25克
相关试题

