【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
参考答案:
【答案】(1)排球50元,篮球80元;(2)①y=-30m+4800 ;m=34、35、36、37、38; ②排球38个,篮球22个时,费用最低为3660.
【解析】
设每个排球需要x元,每个篮球的价格是y元,根据题意列出方程组![]() ,解方程组即可求解;(2)①设购买排球m个,则购买篮球(60-m)个,根据“一次性购买排球和篮球共60个,总费用不超过3 800元”不等式组,解不等式组求得m的取值范围,再结合买排球的个数少于39个即可求得m的具体数值;根据“买排球的总费用+买篮球的总费用=y”即可求得y关于m的函数关系式;②根据排球比较便宜,可知购买排球越多,总费用越低,由此即可解答.
,解方程组即可求解;(2)①设购买排球m个,则购买篮球(60-m)个,根据“一次性购买排球和篮球共60个,总费用不超过3 800元”不等式组,解不等式组求得m的取值范围,再结合买排球的个数少于39个即可求得m的具体数值;根据“买排球的总费用+买篮球的总费用=y”即可求得y关于m的函数关系式;②根据排球比较便宜,可知购买排球越多,总费用越低,由此即可解答.
(1)设每个排球需要x元,每个篮球的价格是y元,
由题意得:![]() ,
,
解得: ![]() ,
,
∴购买一个排球的价格是50元,每个篮球的价格为80元.
(2)①设购买排球m个,则购买篮球(60-m)个,由题意得:
50m+80(60-m)≤3800,
解得m≥![]() ;
;
∵排球的个数少于39个,
∴m<39,
∴排球的个数可以为34,35,36,37,38.
∵总费用为y元,
∴y=50m+80(60-m)=-30m+4800.
②∵排球比较便宜,
∴购买排球越多,总费用越低,
∴当购买排球38个,篮球22个时,费用最低,此时的费用为38×50+22×80=1900+1760=3660(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户种植一种经济作物,总用水量y(m3)与种植时间x(天)之间的函数关系如图所示.
(1)第20天的总用水量为 m3;
(2)当x≥20时,求y与x之间的函数表达式;
(3)种植时间为多少天时,总用水量达到7 000 m3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的图象经过点(0,﹣3),(2,5),(﹣1,﹣4)且与x轴交于A、B两点,其顶点为P.

(1)试确定此二次函数的解析式;
(2)根据函数的图象,指出函数的增减性,并直接写出函数值y<0时自变量x的取值范围.
(3)求△ABP的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字,然后回答下列问题:
已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算
MN=
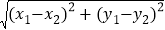 .
.例如:已知P(3,1)、Q(1,-2),则这两点的距离PQ=
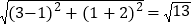 .特别地,如果两点M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为MN=|x1-x2|或|y1-y2|.
.特别地,如果两点M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为MN=|x1-x2|或|y1-y2|.(1)已知A(1,2)、B(-2,-3),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的同一条直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A、B两点间的距离;
(3)已知△ABC的顶点坐标分别为A(0,4)、B(-1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
相关试题

