【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
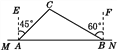
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
参考答案:
【答案】(1)MN不会穿过原始森林保护区,理由见解析;(2)原计划完成这项工程需要25天.
【解析】试题分析:(1)要求MN是否穿过原始森林保护区,也就是求C到MN的距离.要构造直角三角形,再解直角三角形;
(2)根据题意列方程求解.
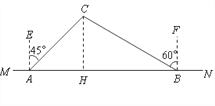
试题解析:(1)如图,过C作CH⊥AB于H,
设CH=x,由已知有∠EAC=45°, ∠FBC=60°
则∠CAH=45°, ∠CBA=30°,在RT△ACH中,AH=CH=x,在RT△HBC中, tan∠HBC=![]()
∴HB=![]() =
=![]() =
=![]() x,
x,
∵AH+HB=AB
∴x+![]() x=600解得x≈220(米)>200(米).∴MN不会穿过森林保护区.
x=600解得x≈220(米)>200(米).∴MN不会穿过森林保护区.
(2)设原计划完成这项工程需要y天,则实际完成工程需要y-5
根据题意得: ![]() =(1+25%)×
=(1+25%)×![]() ,解得:y=25知:y=25的根.
,解得:y=25知:y=25的根.
答:原计划完成这项工程需要25天.
-
科目: 来源: 题型:
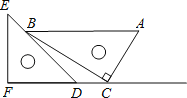
查看答案和解析>>【题目】一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm。

求:(1)FC的长;
(2)EF的长。
-
科目: 来源: 题型:
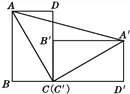
查看答案和解析>>【题目】如图,将竖直放置的长方形砖块ABCD推倒至长方形A'B'C'D'的位置,长方形ABCD的长和宽分别为a,b,AC的长为c.
(1)你能用只含a,b的代数式表示S△ABC,S△C'A'D'和S直角梯形A'D'BA吗?能用只含c的代数式表示S△ACA'吗?
(2)利用(1)的结论,你能验证勾股定理吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题:
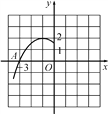
(1)抛物线与x轴的一个交点A的坐标是 ,则抛物线与x轴的另一个交点B的坐标是 ;
(2)确定a的值;
(3)设抛物线的顶点是P,试求△PAB的面积.
-
科目: 来源: 题型:
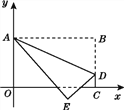
查看答案和解析>>【题目】如图,将长方形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将长方形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,点B的坐标为_________,点E的坐标为_________;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】金瑞公司决定从厂家购进甲、乙两种不同型号的显示器共50台,购进显示器的总金额不超过77000元,已知甲、乙型号的显示器价格分别为1000元/台、2000元/台.
(1)求金瑞公司至少购进甲型显示器多少台?
(2)若甲型显示器的台数不超过乙型显示器的台数,则有哪些购买方案?
相关试题

