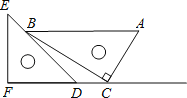
【题目】一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
参考答案:
【答案】15﹣5![]() .
.
【解析】
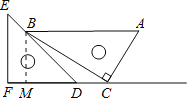
试题分析:过点B作BM⊥FD于点M,根据题意可求出BC的长度,然后在△EFD中可求出∠EDF=45°,进而可得出答案.
解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC×tan60°=10![]() ,
,
∵AB∥CF,
∴BM=BC×sin30°=10![]() ×
×![]() =5
=5![]() ,
,
CM=BC×cos30°=15,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5![]() ,
,
∴CD=CM﹣MD=15﹣5![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
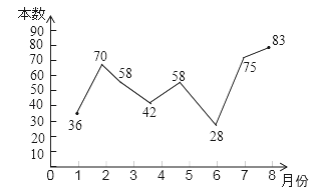
A. 阅读数量的平均数是57 B. 阅读数量的众数是42
C. 阅读数量的中位数是58 D. 有4个月的阅读数量超过60本
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式2x2﹣4xy+2y2因式分解的结果为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A. 2a+3b=5abB. 3ab2﹣3a2b=0
C. x3+2x2=3x5D. 2y2+y2=3y2
-
科目: 来源: 题型:
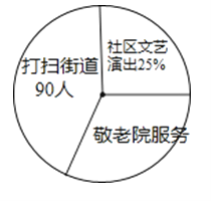
查看答案和解析>>【题目】今年3月5日,某中学组织六、七年级200位学生参与了“走出校门,服务社会”的活动,该校某数学学习小组的同学对那天参与打扫街道、敬老院服务和社区文艺演出的三组人数进行分别统计,部分数据如图所示:
(1)参与社区文艺演出的学生人数是________人,参与敬老院服务的学生人数是________人;
(2)该数学学习小组的同学还发现,六、七年级参与打扫街道的学生人数分别比参与敬老院服务的学生人数多了40%和60%,求参与敬老院服务的六、七年级学生分别有________人 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a+a=a2B.(2a)3=6a3C.(a-1)2=a2-1D.a3÷a=a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=12,求DE的长及四边形ADEF的面积.
相关试题

