【题目】金瑞公司决定从厂家购进甲、乙两种不同型号的显示器共50台,购进显示器的总金额不超过77000元,已知甲、乙型号的显示器价格分别为1000元/台、2000元/台.
(1)求金瑞公司至少购进甲型显示器多少台?
(2)若甲型显示器的台数不超过乙型显示器的台数,则有哪些购买方案?
参考答案:
【答案】(1)23台;(2)①购进甲型显示器23台,乙型显示器27台;②购进甲型显示器24台,乙型显示器26台;③购进甲型显示器25台,乙型显示器25台.
【解析】
试题分析:(1)首先设金瑞公司购进甲型显示器x台,则购进乙型显示器(50-x)台,根据总金额列出不等式,从而得出x的取值范围;(2)根据两种显示器的数量列出不等式,结合第一题得出x的取值范围,从而得出购买方案.
试题解析:(1)设金瑞公司购进甲型显示器![]() 台,则购进乙型显示器
台,则购进乙型显示器![]() 台.依题意得
台.依题意得
![]() ≤
≤![]() 解得
解得![]() ≥
≥![]() 即金瑞公司至少购进甲型显示器23台;
即金瑞公司至少购进甲型显示器23台;
(2)依题意可得不等式![]() ≤
≤![]()
![]() ,解是
,解是![]() ≤
≤![]() , ∴
, ∴![]() ≤
≤![]() ≤
≤![]() .
.
∵![]() 为整数,∴
为整数,∴![]() 可取23、24、25.
可取23、24、25.
①购进甲型显示器23台,乙型显示器27台;
②购进甲型显示器24台,乙型显示器26台;
③购进甲型显示器25台,乙型显示器25台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车收费标准是:起步价10元,可乘3千米;3千米到5千米,每千米1.3元;超过5千米,每千米2.4元。
(1)若某人乘坐了
 (
( )千米的路程,则他应支付的费用是多少?
)千米的路程,则他应支付的费用是多少?(2)若某人乘坐的路程为6千米,那么他应支付的费用是多少?
-
科目: 来源: 题型:
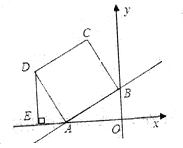
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=0.5x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,过点D作DE⊥x轴,垂足为E.
(1)求点A、B的坐标,并求边AB的长;
(2)求点D的坐标;
(3)你能否在x轴上找一点M,使△MDB的周长最小?如果能,请求出M点的坐标;如果不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.

(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式?
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王从A地前往B地,到达后立刻返回.他与A地的距离y(千米)和所用时间x(小时)之间的函数关系如图所示.
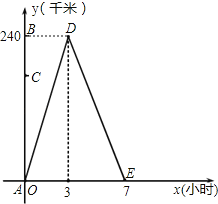
(1)小王从B地返回到A地用了多少小时?
(2)求小王出发6小时后距A地多远?
(3)在A、B之间有一C地,小王从去吋途经C地,到返回时路过C地,共用了2小时20分,求A、C 两地相距多远?
-
科目: 来源: 题型:
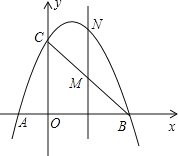
查看答案和解析>>【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N若点M的横坐标为m,请用m的代数式表示MN的长。
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在促销期间规定:商场内所有商品按标价的80%出售,同时当顾客在该商场消费满一定金额后,按如下方案获得相应金额的奖券:
消费金额a(元)范围
200≤a<400
400≤a<500
500≤a<700
700≤a<900
…
获得奖券的金额(元)
30
60
100
130
…
根据上述促销方法,顾客在商场内购物可以获得双重优惠。例如,购买标价为450元的商品,则消费金额为
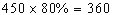 元,获得的优惠额为450×(1-80%)+30=120元,设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价。
元,获得的优惠额为450×(1-80%)+30=120元,设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价。(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在500元与800元之间(含500元和800元)的商品,顾客购买标价为多少元的商品,可以得到
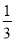 的优惠率?
的优惠率?
相关试题

