【题目】如图(1),在矩形ABCD中,BC=8,点P是BC边上一点,且BP=3,点E是线段CD上的一个动点,把△PCE沿PE折叠,点C的对应点为点F,当点E与点D重合时,点F恰好落在AB上.
(1)求CD的长;
(2)若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;
(3)请直接写出AF的最小值.


参考答案:
【答案】(1)10;(2)y=![]() (或
(或![]() );(3)
);(3)![]() .
.
【解析】
如图1中,设CD=x,由折叠可知:![]() ,在RT△PBF中,求得AF=x-4,在RT△AFD中,根据AD2+AF2=DF2,构建方程即可解决问题.
,在RT△PBF中,求得AF=x-4,在RT△AFD中,根据AD2+AF2=DF2,构建方程即可解决问题.
如下图2所示,MN是线段AD的中垂线,作FG⊥CD于H.设CE=y,根据RT△PNF,求得FN=![]() , CG=FN,GE=
, CG=FN,GE=![]() -y,在RT△GEF中,根据FG2+GE2=EF2,构建方程即可解决问题.
-y,在RT△GEF中,根据FG2+GE2=EF2,构建方程即可解决问题.
要使AF最小,当且仅当点A、F、P在同一直线上.
(1)当点E与点D重合时,如图

设CD=x,
由折叠可知:DF=DC=x, PC=PF=5,
在RT△PBF中,
BF=![]()
则 AF=x-4,
在RT△AFD中,∠A=90°
由AD2+AF2=DF2
得![]()
解得:x=10,即CD=10.
(2)当点F落在AD得中垂线MN上时,
作FG⊥DC于点G,则FG=4,

在RT△PNF中,
FN=![]()
设CE=y,∵CG=FN=![]() ,
,
∴GE=![]() -y,
-y,
在RT△GEF中,由FG2+GE2=EF2
得:42+(![]() -y)2=y2
-y)2=y2
解之得:y=![]() (或
(或![]() )
)
![]()
![]()
要使AF最小,当且仅当点A、F、P在同一直线上
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,该抛物线与x轴的一个交点为(﹣1,0),请回答以下问题.

(1)求抛物线与x轴的另一个交点坐标;
(2)一元二次方程ax2+bx+c=0(a≠0)的解为;
(3)不等式ax2+bx+c<0(a≠0)的解集是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:

(1)旋转中心是点 , 旋转的最小角度是度
(2)AC与EF的位置关系如何,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,
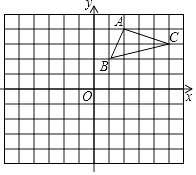
(1)①画出△ABC关于x轴对称的△A1B1C1 .
②画出△ABC绕原点O旋转180°后的△A2B2C2 , 并写出A2、B2、C2的坐标
(2)假设每个正方形网格的边长为1,求△A1B1C1的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=2x2+bx﹣1.
(1)若两点P(﹣3,m)和Q(1,m)在该函数图象上.求b、m的值;
(2)设该函数的顶点为点B,求出点B 的坐标并求三角形BPQ的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第2018个图形中等边三角形的个数是_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.
(1)当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,直接写出结论:AE DB
(填“>”,“<”或“=”).
(2)证明你得出的以上(1),如图2,过点E作EF∥BC,交AC于点F.

(3)在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED = EC.若△ABC的边长为1,AE = 2,求CD的长.
相关试题

