【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,该抛物线与x轴的一个交点为(﹣1,0),请回答以下问题. 
(1)求抛物线与x轴的另一个交点坐标;
(2)一元二次方程ax2+bx+c=0(a≠0)的解为;
(3)不等式ax2+bx+c<0(a≠0)的解集是 .
参考答案:
【答案】
(1)(3,0)
(2)x1=﹣1,x2=3
(3)x<-1或x>3
【解析】解:(1)∵该抛物线与x轴的一个交点为(﹣1,0),抛物线对称轴为直线x=1,
∴抛物线与x轴的另一个交点坐标为:(3,0);
所以答案是:(3,0);(2)∵抛物线与x轴的交点坐标为:(﹣1,0),(3,0),
故一元二次方程ax2+bx+c=0(a≠0)的解为:x1=﹣1,x2=3;
所以答案是:x1=﹣1,x2=3;(3)如图所示:不等式ax2+bx+c<0(a≠0)的解集是:﹣1>x或x>3.
所以答案是:x<-1或x>3.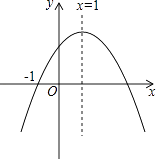
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
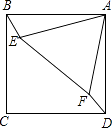
查看答案和解析>>【题目】如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】野营活动中,小明用一张等腰三角形的铁皮代替锅,烙一块与铁皮形状、大小相同的饼,烙好一面后把饼翻身,这块饼能正好落在“锅”中.小丽有五张三角形的铁皮(如图所示),她想选择其中的一张铁皮代替锅,烙一块与所选铁皮形状、大小相同的饼.
(1)五张铁皮中,用序号为_______的铁皮烙饼,不用刀切即可翻身正好落在“锅”中;
(2)在余下的铁皮中选出只需要切一刀(沿直线切饼,下同),然后把两小块饼都翻身,它们正好也能落在“锅”中的铁皮,画出切割线,标上角的度数.

(3)小明最后拿到的是一张图形的三角形铁皮,它既不是等腰三角形又不是直角三角形,也不知道各个角的度数,请在图中画出刀痕的位置(不超过3刀),也能使饼翻身后正好落在“锅”中.(不要写画法,但要用适当的记号或文字作简要说明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:

(1)旋转中心是点 , 旋转的最小角度是度
(2)AC与EF的位置关系如何,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,
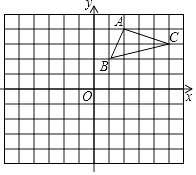
(1)①画出△ABC关于x轴对称的△A1B1C1 .
②画出△ABC绕原点O旋转180°后的△A2B2C2 , 并写出A2、B2、C2的坐标
(2)假设每个正方形网格的边长为1,求△A1B1C1的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在矩形ABCD中,BC=8,点P是BC边上一点,且BP=3,点E是线段CD上的一个动点,把△PCE沿PE折叠,点C的对应点为点F,当点E与点D重合时,点F恰好落在AB上.
(1)求CD的长;
(2)若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;
(3)请直接写出AF的最小值.


相关试题

