【题目】已知:如图,∠1=∠2,∠3=∠E.试说明:∠A=∠EBC.(请按图填空,并补理由.)
证明:∵∠1=∠2 (已知),

∴________∥_______( ),
∴∠E=∠_______ ( ),
又∵∠E=∠3 (已知),
∴∠3=∠____________ ( 等量代换 ),
∴_________∥________ (内错角相等,两直线平行),
∴∠A=∠EBC ( ).
参考答案:
【答案】详见解析.
【解析】
根据平行线的判定定理和平行线的性质进行填空.
证明:∵∠1=∠2 (已知),
∴___BD___∥___CE____ (内错角相等,两直线平行),
∴∠E=∠___4____ (两直线平行,内错角相等),
又∵∠E=∠3 (已知),
∴∠3=∠ 4 ( 等量代换 ),
∴ AD ∥ BE (内错角相等,两直线平行),
∴∠A=∠EBC (两直线平行,同位角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,已知∠B和∠C的平分线相交于点F,经过点F作DE//BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为( )
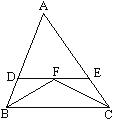
A. 9 B. 8 C. 7 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
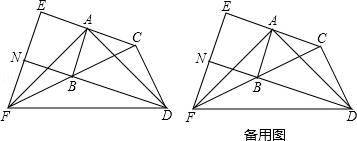
(1)求证:AD=AF;
(2)试判断四边形ABNE的形状,并说明理由. -
科目: 来源: 题型:
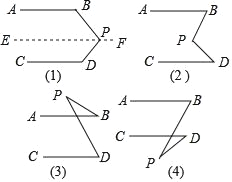
查看答案和解析>>【题目】如图(1),AB∥CD,试求∠BPD与∠B、∠D的数量关系,说明理由.
(1)填空:
解:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB
∴ (如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∠EPD+ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(2)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的数量关系,并说明理由.
(3)观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的数量关系,不用说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

-
科目: 来源: 题型:
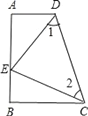
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,这是一个“数值转换机”(箭头为数进入转换机的路径,方框是对进入的数进行转换的转换机).
(1)当输入7、-2018这两个数时,求出它们各自输出的结果;

(2)若输入一非零数,其输出结果为0,则输入的数是多少?(找一个即可)
(3)若输出的结果是2,请直接写出输入的数.(用含自然数n的代数式表示)
相关试题

