【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N. 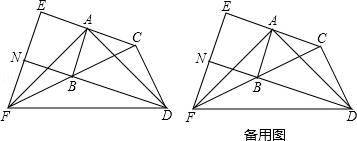
(1)求证:AD=AF;
(2)试判断四边形ABNE的形状,并说明理由.
参考答案:
【答案】
(1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠ABF=135°,
∵∠BCD=90°,
∴∠ABF=∠ACD,
∵CB=CD,CB=BF,∴BF=CD,
在△ABF和△ACD中,
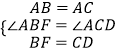 ,
,
∴△ABF≌△ACD(SAS),
∴AD=AF
(2)解:四边形ABNE是正方形;理由如下:
证明:由(1)知,AF=AD,△ABF≌△ACD,
∴∠FAB=∠DAC,
∵∠BAC=90°,
∴∠EAB=∠BAC=90°,
∴∠EAF=∠BAD,
在△AEF和△ABD中, 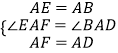 ,
,
∴△AEF≌△ABD△AEF≌△ABD(SAS),
∴BD=EF;
∵CD=CB,∠BCD=90°,
∴∠CBD=45°,
∵∠EAB=90°,△AEF≌△ABD,
∴∠AEF=∠ABD=90°,
∴四边形ABNE是矩形,
又∵AE=AB,
∴四边形ABNE是正方形
【解析】(1)由等腰直角三角形的性质得出∠ABC=∠ACB=45°,求出∠ABF=135°,∠ABF=∠ACD,证出BF=CD,由SAS证明△ABF≌△ACD,即可得出AD=AF;(2)由全等三角形的性质得出得出∠AEF=∠ABD=90°,证出四边形ABNE是矩形,由AE=AB,即可得出四边形ABNE是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A,点B,点C表示的数分别为﹣2,1,6.
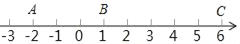
(1)线段AB的长度为 个单位长度,线段AC的长度为 个单位长度.
(2)点P是数轴上的一个动点,从A点出发,以每秒1个单位长度的速度,沿数轴的正方向运动,运动时间为t秒(0≤t≤8).用含t的代数式表示:线段BP的长为 个单位长度,点P在数轴上表示的数为 ;
(3)点M,点N都是数轴上的动点,点M从点A出发以每秒4个单位长度的速度运动,点N从点C出发以每秒3个单位长度的速度运动.设点M,N同时出发,运动时间为x秒.点M,N相向运动,当点M,N两点间的距离为13个单位长度时,求x的值,并直接写出此时点M在数轴上表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,已知∠B和∠C的平分线相交于点F,经过点F作DE//BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为( )
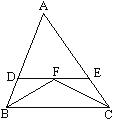
A. 9 B. 8 C. 7 D. 6
-
科目: 来源: 题型:
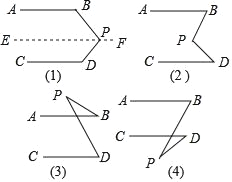
查看答案和解析>>【题目】如图(1),AB∥CD,试求∠BPD与∠B、∠D的数量关系,说明理由.
(1)填空:
解:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB
∴ (如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∠EPD+ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(2)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的数量关系,并说明理由.
(3)观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的数量关系,不用说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,∠3=∠E.试说明:∠A=∠EBC.(请按图填空,并补理由.)
证明:∵∠1=∠2 (已知),

∴________∥_______( ),
∴∠E=∠_______ ( ),
又∵∠E=∠3 (已知),
∴∠3=∠____________ ( 等量代换 ),
∴_________∥________ (内错角相等,两直线平行),
∴∠A=∠EBC ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

相关试题

