搜索
【题目】如图，已知二次函数y=ax2+2x+c图象经过点A （1，4）和点C （0，3）．
（1）求该二次函数的解析式；
（2）结合函数图象，直接回答下列问题：
①当﹣1＜x＜2时，求函数y的取值范围： ．
②当y≥3时，求x的取值范围： ．
参考答案：
【答案】（1）y=﹣x2+2x+3；（2）0＜y≤4，0≤x≤2．
【解析】
(1)把A点和C点坐标代入y=ax2+2x+c得到二元一次方程组,然后解方程组求出a、c即可得到抛物线解析式；
(2)①先分别计算出x为-1和2时的函数值,然后根据二次函数的性质写出对应的函数值的范围;②先计算出函数值为3所对应的自变量的值,然后根据二次函数的性质写出y≥3时,x的取值范围.
（1）将点A和点C的坐标代入函数解析式，得
，
解得
，
二次函数的解析式为y=﹣x2+2x+3；
（2）由图象知，①当﹣1＜x＜2时，求函数y的取值范围：0＜y≤4．
②当y≥3时，求x的取值范围：0≤x≤2．
故答案为：0＜y≤4，0≤x≤2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司生产某种产品的成本是200元/件，售价是250元/件，年销售量为10万件．为了获得更好的效益，公司准备拿出一定的资金做广告．根据经验，每年投入的广告费用x万元，产品的年销售量将是原销售量的y倍，且y与x之间满足二次函数关系：y=﹣0.001x2+0.06x+1．
（1）如果把利润看作是销售总额减去成本费用和广告费用，试求出年利润S（万元）与广告费用x（万元）的函数关系式（无需自变量的取值范围）；
（2）如果公司年投入的广告费不低于10万元且不高于50万元，求年利润S的最大值；
（3）若公司希望年利润在776万元到908万元之间（含端点），请从节约支出的角度直接写出广告费x的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠B=90°，AB=12，BC=24，动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动，动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动，如果点P、Q分别从点A、B同时出发，那么△PBQ的面积S随出发时间t（s）如何变化？写出函数关系式及t的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学初中学生要租车去清华中学参加学习交流活动。已知出租汽车公司有甲、乙两种客车，租1辆甲型客车和2辆乙型客车每人一座可恰好坐162人；租用2辆甲型客车和1辆乙型客车每人一座恰好坐144人，出租公司的租金价格如下：甲型320元/辆，乙型460元/辆。大江中学共有660名师生，学校准备支付的租车的费用最多是5320元。
（1）求甲、乙两种型号的客车每辆各有多少个座位；
（2）若要租用甲、乙共14辆，怎样租车费用最低，并求出租车最低费用。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，矩形ABCD中，延长BC至E，连接DE，F为DE的中点，连结AF、CF且AF⊥CF.
求证：(1)∠ADF=∠BCF；
(2)BD=AD+CE.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在
中，
、
、
三边的长分别为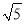
、
、
，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点（即三个顶点都在小正方形的顶点处），如图①所示．这样不需求的高，而借用网格就能计算出它的面积．（1）请你将
的面积直接填写在横线上．__________________（2）我们把上述求
面积的方法叫做构图法．若三边的长分别为
、
、
（
），请利用图②的正方形网格（每个小正方形的边长为
）画出相应的，并求出它的面积．（3） 若△ABC三边的长分别为
、
、
(m＞0，n＞0，且m≠n)，请利用图③的长方形网格试运用构图法求出这三角形的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数
的图象与x轴、y轴分别交于A、B，以线段AB为直角边在第一象限内作Rt△ABC，且使∠ABC=30°。（1）求AC的长度；
（2）如果在第二象限内有一点
，试求四边形AOPB的面积S与m之间的函数关系式，并求当△APB与△ABC面积相等时m的值。（3）是否存在使△QAB是等腰三角形并且在坐标轴上的点Q？若存在，请写出点Q所有可能的坐标；若不存在，请说明理由。
相关试题
