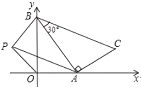
【题目】如图,一次函数![]() 的图象与x轴、y轴分别交于A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°。
的图象与x轴、y轴分别交于A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°。
(1)求AC的长度;
(2)如果在第二象限内有一点 ,试求四边形AOPB的面积S与m之间的函数关系式,并求当△APB与△ABC面积相等时m的值。
,试求四边形AOPB的面积S与m之间的函数关系式,并求当△APB与△ABC面积相等时m的值。
(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由。

参考答案:
【答案】(1)AC=![]() ;(2)m=
;(2)m=![]() ;(3)(0,
;(3)(0,![]() 2),(0,
2),(0,![]() +2),(1,0)(3,0),(0,
+2),(1,0)(3,0),(0,![]() ),(0,
),(0,![]() )
)
【解析】
(1)先求出A、B两点的坐标,再由一个角等于30°,即可求出AC的长;
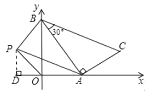
(2)过P作PD⊥x轴,垂足为D,先求出梯形ODPB的面积和△AOB的面积之和,再减去△APD的面积,即是△APB的面积;根据△APB与△ABC面积相等,求得m的值;
(3)假设存在点Q,使△QAB是等腰三角形,分情况求出Q点的坐标即可.
(1)∵一次函数的解析式为![]() 函数图象与x轴、y轴分别交于点A、B,
函数图象与x轴、y轴分别交于点A、B,
∴A(1,0),B(0,![]() ),
),
∴AB=2,
设AC=x,则BC=2x,由勾股定理得,4x2x2=4,
解得x=![]()
则AC=![]() ;
;
(2)过P作PD⊥x轴,垂足为D,
S△APB=S梯形ODPB+S△AOBS△APD=
=![]() ,
,
∵S△ABC=
∴![]() =
=![]()
解得m=![]() ;
;
(3)∵AB=![]() =2,
=2,
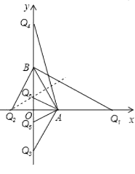
∴如图:当AQ=AB时,点Q1(3,0),Q2(1,0),Q3(0,![]() );
);
当AB=BQ时,点Q4(0,![]() +2),Q5(0,
+2),Q5(0,![]() 2),Q2(1,0);
2),Q2(1,0);
当AQ=BQ时,点Q6(0,![]() ),Q2(1,0),
),Q2(1,0),
综上可得:(0,![]() 2),(0,
2),(0,![]() +2),(1,0)(3,0),(0,
+2),(1,0)(3,0),(0,![]() ),(0,
),(0,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+2x+c图象经过点A (1,4)和点C (0,3).
(1)求该二次函数的解析式;
(2)结合函数图象,直接回答下列问题:
①当﹣1<x<2时,求函数y的取值范围: .
②当y≥3时,求x的取值范围: .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,延长BC至E,连接DE,F为DE的中点,连结AF、CF且AF⊥CF.
求证:(1)∠ADF=∠BCF;
(2)BD=AD+CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 、
、 、
、 三边的长分别为
三边的长分别为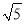 、
、 、
、 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点 (即
(即 三个顶点都在小正方形的顶点处),如图①所示.这样不需求
三个顶点都在小正方形的顶点处),如图①所示.这样不需求 的高,而借用网格就能计算出它的面积.
的高,而借用网格就能计算出它的面积.(1)请你将
 的面积直接填写在横线上.__________________
的面积直接填写在横线上.__________________(2)我们把上述求
 面积的方法叫做构图法.若
面积的方法叫做构图法.若 三边的长分别为
三边的长分别为 、
、 、
、 (
( ),请利用图②的正方形网格(每个小正方形的边长为
),请利用图②的正方形网格(每个小正方形的边长为 )画出相应的
)画出相应的 ,并求出它的面积.
,并求出它的面积.(3) 若△ABC三边的长分别为
 、
、 、
、 (m>0,n>0,且m≠n),请利用图③的长方形网格试运用构图法求出这三角形的面积.
(m>0,n>0,且m≠n),请利用图③的长方形网格试运用构图法求出这三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
 ﹣x﹣3.
﹣x﹣3.(1)用配方法求函数图象顶点坐标、对称轴,并写出图象的开口方向;
(2)在所给网格中建立平面直角坐标系井直接画出此函数的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,海中有一个小岛A,它的周围15海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西60° 的B处,往东航行20海里后到达该岛南偏西30° 的C处后,货船继续向东航行,你认为货船航行途中_____ 触礁的危险.(填写:“有”或“没有”)
参考数据:sin60°=cos30°≈0.866.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 直线
 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点, 点P为OA上一动点, 当PC+PD最小时, 点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点, 点P为OA上一动点, 当PC+PD最小时, 点P的坐标为( )
A.(-4,0)B.(-1,0)C.(-2,0)D.(-3,0)
相关试题

