【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
参考答案:
【答案】
(1)解:由题意可知,50次摸球实验活动中,出现红球20次,黄球30次,
∴红球所占百分比为20÷50=40%,
黄球所占百分比为30÷50=60%,
答:红球占40%,黄球占60%
(2)解:由题意可知,50次摸球实验活动中,出现有记号的球4次,
∴总球数为8÷ ![]() =100,
=100,
∴红球数为100×40%=40,
答:盒中红球有40个
【解析】(1)根据表格数据可以得到50次摸球实验活动中,出现红球20次,黄球30次,由此即可求出盒中红球、黄球各占总球数的百分比;(2)由题意可知50次摸球实验活动中,出现有记号的球4次,由此可以求出总球数,然后利用(1)的结论即可求出盒中红球.
【考点精析】解答此题的关键在于理解用频率估计概率的相关知识,掌握在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩被分别绘制成如下两个统计图:
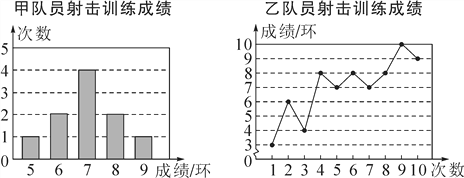
根据以上信息,整理分析数据如下:
平均成绩(环)
中位数(环)
众数(环)
方差
甲
a
7
7
1.2
乙
7
b
8
4.2
(1)则表格中a,b的值分别是a=________,b=________;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c满足|a﹣
 |+
|+ +(c﹣4
+(c﹣4 )2=0.
)2=0.(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界读书日,新华书店矩形购书优惠活动:①一次性购书不超过100元,不享受打折优惠;②一次性购书超过100元但不超过200元一律八折;③一次性购书200元以上一律打六折.小丽在这次活动中,两次购书总共付款190.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)
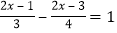 (2)
(2)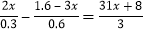 ;
;(3)
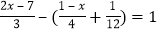 (4)
(4) [x﹣
[x﹣ (x﹣1)]=2(x﹣1)
(x﹣1)]=2(x﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.

(1)求 的长.
的长.
(2)求弦BD的长.
相关试题

