【题目】若关于 x 的一元二次方程axbxc=0(a0,c0,a、b、c为常数)有两个不相等的实数根![]() ,
,![]() (0
(0![]()
![]() ),O为坐标原点,A、B为x轴正半轴上的两点且A
),O为坐标原点,A、B为x轴正半轴上的两点且A![]() ,0,B
,0,B![]() ,0.
,0.
(1)当![]() =c=2,b=-
=c=2,b=-![]() 时,求
时,求![]() 与a的值;
与a的值;
(2)当 x 1,c 6a 时,P为一次函数 y x4图象上一点,Q为平面直角坐标系中的一点,若点 A、B、P、Q 为一个矩形的四个顶点,请确定点Q的坐标;
(3)当![]() =2c时,试问在正比例函数y=
=2c时,试问在正比例函数y=![]() 的图象上是否存在点M使得△ABM为等边三角形?判断并证明你的结论。
的图象上是否存在点M使得△ABM为等边三角形?判断并证明你的结论。

参考答案:
【答案】(1)![]() =3,a=
=3,a=![]() ;(2)点Q的坐标为:(6,3)或(1,-2);(3)不存在点M使得△ABM为等边三角形,证明见解析.
;(2)点Q的坐标为:(6,3)或(1,-2);(3)不存在点M使得△ABM为等边三角形,证明见解析.
【解析】
(1)把![]() =c=2,b=
=c=2,b=![]() 代入可求出a的值,从而得到该方程,利用根与系数的关系可求出另一根;
代入可求出a的值,从而得到该方程,利用根与系数的关系可求出另一根;
(2)把x1,c6a代入可求出b=-7a,从而将方程变形为a(x-1)(x-6)=0,得到A,B坐标,然后根据一次函数图像上点的坐标特征和矩形的性质可分情况求出点Q的坐标;
(3)将![]() =2c代入axbx c=0利用根与系数的关系求出
=2c代入axbx c=0利用根与系数的关系求出![]() ,得到A,B坐标,过点M作MC⊥x轴于点C,由C是AB中点,可求出C的坐标,进而代入正比例函数解析式得到M点坐标,然后根据CM=
,得到A,B坐标,过点M作MC⊥x轴于点C,由C是AB中点,可求出C的坐标,进而代入正比例函数解析式得到M点坐标,然后根据CM=![]() AC列出方程求出b值,推出矛盾,问题得解.
AC列出方程求出b值,推出矛盾,问题得解.
解:(1)把![]() =c=2,b=
=c=2,b=![]() 代入ax bx c=0得:4a+2×(
代入ax bx c=0得:4a+2×(![]() )+2=0,
)+2=0,
解得:a=![]() ,
,
所以该方程为:![]() x
x![]() x 2=0,
x 2=0,
∵![]() =
=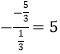 ,即2+
,即2+![]() =5,
=5,
∴![]() =3;
=3;
(2)把x1,c6a代入axbx c=0得ab6a=0,
∴b=-7a;
∴ax-7ax 6a=0,即a(xx 6)=0,
∴a(x-1)(x-6)=0(a0),
∴![]() ,
,![]() ,
,
∴A(1,0),B(6,0),
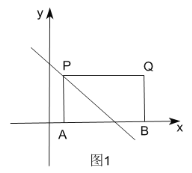
①如图1,过点A作AP⊥x轴交直线yx4于点P,
∴P(1,3),
∵四边形APQB为矩形,
∴Q(6,3);
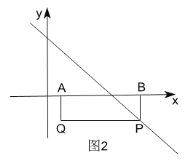
②如图2,过点B作BP⊥x轴交直线yx4于点P,
∴P(6,-2),
∵四边形ABPQ为矩形,
∴Q(1,-2);
综上所述,点Q的坐标为:(6,3)或(1,-2);
(3)不存在点M使得△ABM为等边三角形;
证明:将![]() =2c代入axbx c=0得:4ac2+2bc+c=0,即c(4ac+2b+1)=0,
=2c代入axbx c=0得:4ac2+2bc+c=0,即c(4ac+2b+1)=0,
∵c0,
∴4ac+2b+1=0①,
∵![]() ,
,
∴![]() ,
,
∴A(2c,0),B(![]() ,0),
,0),
假设存在点M使得△ABM为等边三角形,
如图3,过点M作MC⊥x轴于点C,则C是AB中点,
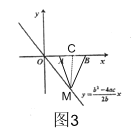
∴C点横坐标为:![]() ,
,
将![]() 代入
代入![]() 可得
可得![]() ,
,
由①可知4ac=-(2b+1),4ac+1=-2b,
∴![]() ,
,
∴M(![]() ,
,![]() ),
),
当△ABM为等边三角形时,CM=![]() AC,
AC,
AC![]() ,
,
∴![]()
∴![]() ,
,
解得:b=-1(舍)或b=![]() ,
,
∵b=![]() ,
,![]() ,
,
∴a<0,与题设中a0矛盾,
∴不存在点M使得△ABM为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

-
科目: 来源: 题型:
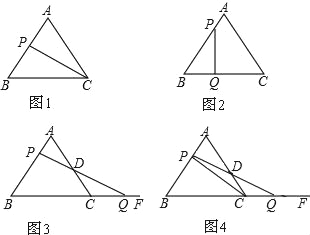
查看答案和解析>>【题目】已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A出发,沿线段AB向点B运动.
(1)如图1,设点P的运动时间为t(s),那么t= (s)时,△PBC是直角三角形;
(2)如图2,若另一动点Q从点B出发,沿线段BC向点C运动,如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△PBQ是直角三角形?
(3)如图3,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D.如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△DCQ是等腰三角形?
(4)如图4,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D,连接PC.如果动点P、Q都以1cm/s的速度同时出发.请你猜想:在点P、Q的运动过程中,△PCD和△QCD的面积有什么关系?并说明理由.
-
科目: 来源: 题型:
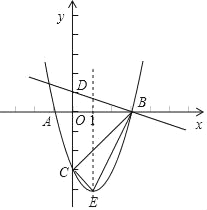
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,直线y=﹣
 x+1与y轴交于点D.
x+1与y轴交于点D.(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利民商场经营某种品牌的T恤,购进时的单价是300元,根据市场调查:在一段时间内,销售单价是400元时,销售量是60件,销售单价每涨10元,销售量就减少1件.设这种T恤的销售单价为x元(x>400)时,销售量为y件、销售利润为W元.
(1)请分别用含x的代数式表示y和W(把结果填入下表):
销售单价(元)
x
销售量y(件)
销售利润W(元)
(2)该商场计划实现销售利润10000元,并尽可能增加销售量,那么x的值应当是多少?
-
科目: 来源: 题型:
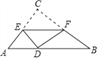
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.翻折∠C,使点C落在斜边上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若△CEF与△ABC相似,则AD的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
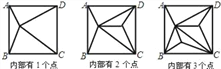
(1)填写下表:
正方形ABCD内点的个数
1
2
3
4
…
n
分割成的三角形的个数
4
6
…
(2)原正方形能否被分割成2008个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
相关试题

