搜索
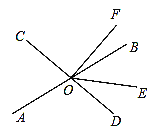
【题目】如图，直线AB、CD相交于点O．已知∠BOD＝75°，OE把∠AOC分成两个角，且∠AOE：∠EOC＝2：3．
（1）求∠AOE的度数；
（2）若OF平分∠BOE，问：OB是∠DOF的平分线吗？试说明理由．
参考答案：
【答案】(1) 30°；(2) OB是∠DOF的平分线,理由见解析
【解析】
（1）设∠AOE＝2x，根据对顶角相等求出∠AOC的度数，根据题意列出方程，解方程即可；
（2）根据角平分线的定义求出∠BOF的度数即可．
（1）∵∠AOE：∠EOC＝2：3．∴设∠AOE＝2x，则∠EOC＝3x，∴∠AOC＝5x．
∵∠AOC＝∠BOD＝75°，∴5x＝75°，解得：x＝15°，则2x＝30°，∴∠AOE＝30°；
（2）OB是∠DOF的平分线．理由如下：
∵∠AOE＝30°，∴∠BOE＝180°﹣∠AOE＝150°．
∵OF平分∠BOE，∴∠BOF＝75°．
∵∠BOD＝75°，∴∠BOD＝∠BOF，∴OB是∠DOF的角平分线．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校九（1）、九（2）两班的班长交流了为四川安雅地震灾区捐款的情况：
（Ⅰ）九（1）班班长说：“我们班捐款总数为1200元，我们班人数比你们班多8人．”
（Ⅱ）九（2）班班长说：“我们班捐款总数也为1200元，我们班人均捐款比你们班人均捐款多20%．”
请根据两个班长的对话，求这两个班级每班的人均捐款数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB、CD相交于点O，∠BOM=90°，∠DON=90°．
（1）若∠COM=∠AOC，求∠AOD的度数；
（2）若∠COM=
∠BOC，求∠AOC和∠MOD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB、CD交于点O，OM⊥AB，
（1）若∠1=∠2，试判断ON与CD的位置关系，并说明理由.
（2）若∠1=
∠BOC，试求∠MOD的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是边长为6的正方形，点E在边AB上，BE＝4，过点E作EF∥BC，分别交BD、CD于G、F两点．若M、N分别是DG、CE的中点，则MN的长为 （ ）
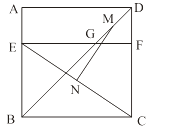
A.3
B.
C.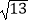
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】将两个斜边长相等的直角三角形纸片如图①放置，其中∠ACB=∠CED=90°．∠A=45°，∠D=30°．
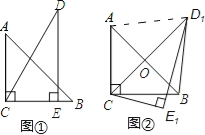
（1）∠CBA= ；
（2）把△DCE绕点C顺时针旋转15°得到△D1CE1，如图②，连接D1B，则∠E1D1B= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线AB、CD相交于点O，OE平分∠BOD．OF⊥CD，垂足为O，若∠EOF＝54°．
（1）求∠AOC的度数；
（2）作射线OG⊥OE，试求出∠AOG的度数．
相关试题
