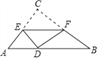
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.翻折∠C,使点C落在斜边上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若△CEF与△ABC相似,则AD的长为_____.
参考答案:
【答案】![]() 或
或![]()
【解析】分析:若△CEF与△ABC相似,分两种情况:①若若CE:CF=3:4,如图1所示,此时EF∥AB. CD为AB边上的高,②若CF:CE=3:4,如图2所示.由相似三角形角之间的关系,可以推出∠A=∠ECD,与∠CEF=∠B.从而得到![]() ,即D点为AB的中点.
,即D点为AB的中点.
详解:若△CEF与△ABC相似,分两种情况:
若CE:CF=3:4,如图1所示:

∵CE:CF=AC:BC,
∴EF∥AB.
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高,
在Rt△ABC中,∵![]()
∴![]()
∴![]()
∴AD=ACcosA=![]()
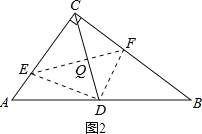
若CF:CE=3:4,如图2所示:
∵△CEF∽△CBA,
∴∠CEF=∠B.
由折叠性质可知,![]()
又∵![]()
∴∠A=∠ECD,
∴AD=CD.
同理可得:∠B=∠FCD,CD=BD,
∴D点为AB的中点,
∴![]()
综上所述,AD的长为![]() 或
或![]()
故答案为:![]() 或
或![]()
-
科目: 来源: 题型:
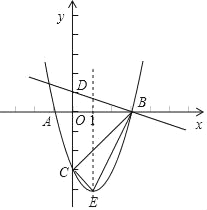
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,直线y=﹣
 x+1与y轴交于点D.
x+1与y轴交于点D.(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于 x 的一元二次方程axbxc=0(a0,c0,a、b、c为常数)有两个不相等的实数根
 ,
, (0
(0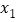
 ),O为坐标原点,A、B为x轴正半轴上的两点且A
),O为坐标原点,A、B为x轴正半轴上的两点且A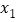 ,0,B
,0,B ,0.
,0.(1)当
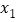 =c=2,b=-
=c=2,b=- 时,求
时,求 与a的值;
与a的值;(2)当 x 1,c 6a 时,P为一次函数 y x4图象上一点,Q为平面直角坐标系中的一点,若点 A、B、P、Q 为一个矩形的四个顶点,请确定点Q的坐标;
(3)当
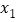 =2c时,试问在正比例函数y=
=2c时,试问在正比例函数y=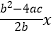 的图象上是否存在点M使得△ABM为等边三角形?判断并证明你的结论。
的图象上是否存在点M使得△ABM为等边三角形?判断并证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】利民商场经营某种品牌的T恤,购进时的单价是300元,根据市场调查:在一段时间内,销售单价是400元时,销售量是60件,销售单价每涨10元,销售量就减少1件.设这种T恤的销售单价为x元(x>400)时,销售量为y件、销售利润为W元.
(1)请分别用含x的代数式表示y和W(把结果填入下表):
销售单价(元)
x
销售量y(件)
销售利润W(元)
(2)该商场计划实现销售利润10000元,并尽可能增加销售量,那么x的值应当是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
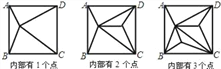
(1)填写下表:
正方形ABCD内点的个数
1
2
3
4
…
n
分割成的三角形的个数
4
6
…
(2)原正方形能否被分割成2008个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小正方形卡片(如图1)不重叠地放在一个底面为长方形(长为mcm,宽为ncm)的盒子的底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分的周长和是( )

A. 4mcmB. 4ncmC. 2(m+n)cmD. 4(mn)cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A地仍要宣传8分钟,那么他们从B地返回学校用的时间是( )

A. 45.2分钟 B. 48分钟 C. 46分钟 D. 33分钟
相关试题

