【题目】在平面直角坐标系xOy中,直线y=2x﹣3与y轴交于点A,点A与点B关于x轴对称,过点B作y轴的垂线l,直线l与直线y=2x﹣3交于点C.
(1)求点C的坐标;
(2)如果抛物线y=nx2﹣4nx+5n(n>0)与线段BC有唯一公共点,求n的取值范围. 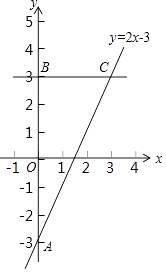
参考答案:
【答案】
(1)解:∵直线y=2x﹣3与y轴交于点A(0,﹣3),
∴点A关于x轴的对称点B(0,3),l为直线y=3,
∵直线y=2x﹣3与直线l交于点C,
∴点C坐标为(3,3),
(2)解:∵抛物线y=nx2﹣4nx+5n(n>0),
∴y=nx2﹣4nx+4n+n=n(x﹣2)2+n(n>0)
∴抛物线的对称轴为直线x=2,顶点坐标为(2,n),
∵点B(0,3),点C(3,3),
①当n>3时,抛物线的最小值为n>3,与线段BC无公共点;
②当n=3时,抛物线的顶点为(2,3),在线段BC上,此时抛物线与线段BC有一个公共点;
③当0<n<3时,抛物线最小值为n,与线段BC有两个公共点;
如果抛物线y=n(x﹣2)2+n经过点B,则3=5n,解得n= ![]() ,
,
由抛物线的对称轴为直线x=2,可知抛物线经过点(4,3),
点(4,3)不在线段BC上,此时抛物线与线段BC有一个公共点B;
如果抛物线y=n(x﹣2)2+n经过点C,则3=2n,解得n= ![]() ,
,
由抛物线的对称轴为直线x=2,可知抛物线经过点(1,3),
点(1,3)在线段BC上,此时抛物线与线段BC有两个公共点;
综上所述,当 ![]() ≤n<
≤n< ![]() 或n=3时,抛物线与线段BC有一个公共点.
或n=3时,抛物线与线段BC有一个公共点.
【解析】(1)根据题意分别求出点A、B、C的坐标;(2)求得抛物线的对称轴,顶点的坐标;再分类讨论①当n>3时;②当n=3时;③当0<n<3时,抛物线y=nx2﹣4nx+5n(n>0)与线段BC有唯一公共点,求n的取值范围.
【考点精析】通过灵活运用一次函数的性质和二次函数的性质,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.
-
科目: 来源: 题型:
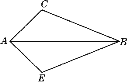
查看答案和解析>>【题目】如图,对角线AB把四边形ACBE分为△ABC和△ABE两部分,如果△ABC中BC边上的高和△ABE中BE边上的高相等,且AC=AE.
(1)在原图上画出△ABC中BC边上的高AD与△ABE中BE边上的高AF;
(2)请你猜想BC与BE的数量关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东根据学习函数的经验,对函数y=
 图象与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
图象与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)如表是y与x的几组对应值.x
…
﹣2
﹣1
﹣

0

1

2

3
4
…
y
…



2

4

2


m
…
表中m的值为;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数y= 的大致图象;
的大致图象; 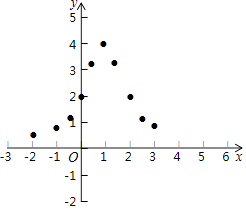
(4)结合函数图象,请写出函数y= 的一条性质.
的一条性质.
(5)解决问题:如果函数y= 与直线y=a的交点有2个,那么a的取值范围是 .
与直线y=a的交点有2个,那么a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】(方程思想)如图,在铁路CD同侧有两个村庄A,B,它们到铁路的距离分别是15 km和10 km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25 km.已知铁路旁有一个农副产品收购站E,且AE=BE,求CE的长.
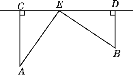
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.

(1)如果点D在线段BC上运动,如图1:
①依题意补全图1;
②求证:∠BAD=∠EDC;
③通过观察、实验,小明得出结论:在点D运动的过程中,总有∠DCE=135°,.
小明与同学讨论后,形成了证明这个结论的几种想法:
想法一:在AB上取一点F,使得BF=BD,要证∠DCE=135°,只需证△ADF≌△DEC.
想法二:以点D为圆心,DC为半径画弧交AC于点F,要证∠DCE=135°,只需证△AFD≌△DCE.
想法三:过点E作BC所在直线的垂直线段EF,要证∠DCE=135°,只需证EF=CF.
…
请你参考上面的想法,证明∠DCE=135°
(2)如果点D在线段CB的延长线上运动,利用图2画图分析,∠DCE的度数还是确定的值吗?如果是,直接写出∠DCE的度数;如果不是,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=
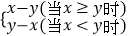 ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
(1)请直接写出点(3,5)的“关联点”的坐标;
(2)如果点P在函数y=x﹣2的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=2x2的图象上,当0≤m≤2时,求线段MN的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

相关试题

