搜索
【题目】解不等式组 
（1）解：解不等式①得：；
（2）解不等式②得：；
（3）把不等式①和②的解集在数轴上表示出来：
（4）所以，这个不等式组的解集是.
参考答案：
【答案】
（1）x<3
（2）x≥-2
（3）
解： 
（4）-2≤x<3
【解析】先求得这个不等式的解集，在数轴上表示出这两个不等式的解集，从而确定不等式组的解集即可.
【考点精析】利用一元一次不等式组的解法和在数轴上表示不等式组的解集对题目进行判断即可得到答案，需要熟知解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )；不等式组的解集可以在数轴上表示出来;当任何数x都不能使不等式同时成立，我们就说这个不等式组无解或其解为空集．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，线段AB ， AD交于点A ． C为直线AD上一点（不与点A ， D重合）．过点C在BC的右侧作射线CE⊥BC ， 过点D作直线DF∥AB ， 交CE于点G（G与D不重合）．
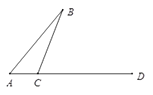
（1）如图1，若点C在线段AD上，且∠BCA为钝角．①按要求补全图形；②判断∠B与∠CGD的数量关系，并证明．
（2）若点C在线段DA的延长线上，请直接写出∠B与∠CGD的数量关系；
（3）请你结合本题的题意提出一个新的拓展问题 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=x2+2x+
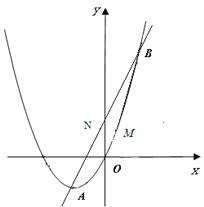
与x轴有两个交点，且k为正整数．（1）求k的值；
（2）当二次函数y=x2+2x+
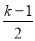图象经过原点时，直线y=3x+2与之交于A、B两点，若M是抛物线上在直线y=3x+2下方的一个动点，△MAB面积是否存在最大值？若存在，请求出M点坐标，并求出△MAB面积最大值；若不存在，请说明理由.（3）将（2）中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分保持不变，翻折后的图象与原图象x轴上方的部分组成一个新图象.若直线y=kx+2（k>0）与该新图象恰好有三个公共点，求k的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在AC⊥BC，过点C的直线MN∥AB，D为AB边上一点，且AD=4，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．
（1）求CE的长；
（2）当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，BE//CD ， ∠A=∠1. 求证：∠C=∠E .
-
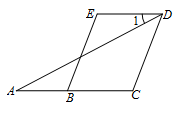
科目： 来源： 题型：
查看答案和解析>>【题目】我区注重城市绿化提高市民生活质量，新建林荫公园计划购买甲、乙两种树苗共800株，甲种树苗每株12元，乙种树苗每株15元．相关资料表明：甲、乙两种树苗的成活率分别为85%、90%．
（1）若购买这两种树苗共用去10500元，则甲、乙两种树苗各购买多少株？
（2）若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？
（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“a<b”的反面应是（ ）
A．a≠b B．a>b C．a=b D．a=b或a>b
相关试题
