搜索
【题目】已知：如图，BE//CD ， ∠A=∠1. 求证：∠C=∠E .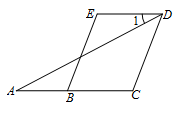
参考答案：
【答案】证明：∵∠A=∠1，
∴DE//AC .
∴∠E=∠EBA .
∵BE//CD ，
∴∠EBA=∠C .
∴∠C=∠E .
【解析】 由∠A=∠1，根据内错角相等，两直线平行可得DE//CA，根据两直线平行，内错角相等可得∠E=∠EBA ；再由BE//CD ，根据两直线平行，同位角相等可得 ∠EBA=∠C ，所以 ∠C=∠E .
【考点精析】本题主要考查了平行线的判定与性质的相关知识点，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=x2+2x+
与x轴有两个交点，且k为正整数．（1）求k的值；
（2）当二次函数y=x2+2x+
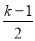图象经过原点时，直线y=3x+2与之交于A、B两点，若M是抛物线上在直线y=3x+2下方的一个动点，△MAB面积是否存在最大值？若存在，请求出M点坐标，并求出△MAB面积最大值；若不存在，请说明理由.（3）将（2）中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分保持不变，翻折后的图象与原图象x轴上方的部分组成一个新图象.若直线y=kx+2（k>0）与该新图象恰好有三个公共点，求k的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在AC⊥BC，过点C的直线MN∥AB，D为AB边上一点，且AD=4，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．
（1）求CE的长；
（2）当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
-
科目： 来源： 题型：
查看答案和解析>>【题目】解不等式组
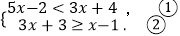
（1）解：解不等式①得：；
（2）解不等式②得：；
（3）把不等式①和②的解集在数轴上表示出来：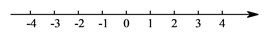
（4）所以，这个不等式组的解集是. -
科目： 来源： 题型：
查看答案和解析>>【题目】我区注重城市绿化提高市民生活质量，新建林荫公园计划购买甲、乙两种树苗共800株，甲种树苗每株12元，乙种树苗每株15元．相关资料表明：甲、乙两种树苗的成活率分别为85%、90%．
（1）若购买这两种树苗共用去10500元，则甲、乙两种树苗各购买多少株？
（2）若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？
（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“a<b”的反面应是（ ）
A．a≠b B．a>b C．a=b D．a=b或a>b
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于三角函数有如下的公式：
sin（α+β）=sinαcosβ+cosαsinβ①；cos（α+β）=cosαcosβ﹣sinαsinβ②；tan（α+β）=
③利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值，
如：tan105°=tan（45°+60°）=
=
=
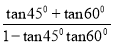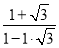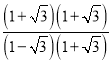=﹣（2+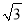
）．根据上面的知识，你可以选择适当的公式解决下面的实际问题：
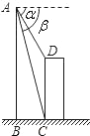
如图，直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°，底端C点的俯角β=75°，此时直升飞机与建筑物CD的水平距离BC为42m，求建筑物CD的高．
相关试题
