【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|2a﹣b+8|+(a+b﹣2)2=0.

(1)求a、b的值;
(2)如图1,点G在y轴上,三角形COG的面积是三角形ABC的面积的![]() ,求出点G的坐标;
,求出点G的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一个动点,连接OP、AC、DB,OE平分∠AOP,OF⊥CE,若∠OPD+k∠DOF=k(∠FOP+∠AOE),现将四边形ABDC向下平移![]() k个单位得到四边形A1B1D1C1,已知AM+BN =
k个单位得到四边形A1B1D1C1,已知AM+BN =![]() k,求图中阴影部分的面积.
k,求图中阴影部分的面积.
参考答案:
【答案】(1)a=﹣2,b=4;(2)G(0,6)或(0,﹣6);(3)S阴=![]() .
.
【解析】
(1)利用非负数的性质即可解决问题;
(2)过点C作CT⊥AB于T.根据面积关系求出OG的长即可解决问题;
(3)设∠AOE=x,则∠AOP=2∠AOE=2x,∠POB=180°-2x,由CD∥AB,推出∠OPD=∠POB=180°-2x,由∠DOF=∠AOE,推出∠OPD+k∠DOF=k∠FOP+k∠AOE,推出∠OPD=k∠FOP,可得180°-2x=k(90°-x),推出k=2,即可解决问题.
(1)∵|2a﹣b+8|+(a+b﹣2)2=0,
又∵|2a﹣b+8|≥0,(a+b﹣2)2≥0,
∴![]() ,
,
解得![]() ,
,
∴a=﹣2,b=4.
(2)如图1中,过点C作CT⊥AB于T.
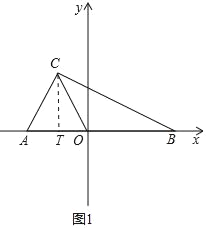
∵C(﹣1,2),
∴CT=2,
∵S△ABC=![]() ×6×2=6,
×6×2=6,
∴S△OCG=![]() ×1×OG=3,
×1×OG=3,
∴OG=6,
∴G(0,6)或(0,﹣6).
(3)如图2中,
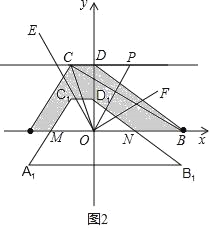
设∠AOE=x,
∵OE平分∠AOP,
∴∠AOP=2∠AOE=2x,
∵∠AOB=180°,
∴∠POB=180°﹣2x,
∵CD⊥y轴,AB⊥y轴,
∴∠CDO=∠DOB=90°,
∴CD∥AB,
∴∠OPD=∠POB=180°﹣2x,
∵OF⊥OE,
∴∠FOP=90°﹣x,
∵∠AOD=90°,
∴∠AOE+∠EOD=∠DOF+∠EOD=90°,
∴∠DOF=∠AOE,
∴∠OPD+k∠DOF=k∠FOP+k∠AOE,
∴∠OPD=k∠FOP,
∴180°﹣2x=k(90°﹣x),
∴k=2,
∴![]() ,
,
∴AM+BN=![]() ,
,
∴S阴=S四边形MNB1A1=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】参照学习函数的过程与方法,探究函数
 的图象与性质.
的图象与性质.因为
 ,即
,即 ,所以我们对比函数
,所以我们对比函数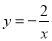 来探究.
来探究.列表:

…






1
2
3
4
…
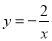
…

1
2
4


1


…

…


2
3
5


0


…
描点:在平面直角坐标系中,以自变量
p>(1)请你把 的取值为横坐标,以
的取值为横坐标,以 相应的函数值为纵坐标,描出了相应的点(如图所示).
相应的函数值为纵坐标,描出了相应的点(如图所示). 轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;(2)观察图象并分析表格,回答下列问题:
①当
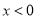 时,
时, 随
随 的增大而 ;(填“增大”或“减小”)
的增大而 ;(填“增大”或“减小”)②
 的图象是由
的图象是由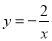 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;③
 图象关于点 成中心对称.(填点的坐标)
图象关于点 成中心对称.(填点的坐标)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
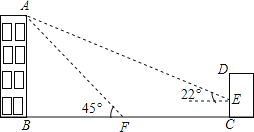
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈
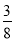 ,cos22°≈
,cos22°≈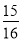 ,tan22°≈
,tan22°≈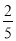 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与反比例函数
的图象与反比例函数 的图象交于
的图象交于 ,
, 两点,与
两点,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,已知点
,已知点 坐标为
坐标为 ,点
,点 的坐标为
的坐标为 .
.(1)求反比例函数的解析式和一次函数的解析式;
(2)连结
 ,求
,求 的面积;
的面积;(3)观察图象直接写出
 时
时 的取值范围是 ;
的取值范围是 ;(4)直接写出:
 为
为 轴上一动点,当三角形
轴上一动点,当三角形 为等腰三角形时点
为等腰三角形时点 的坐标 .
的坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形 ABEF 的面积为 4,△BCE 是等边三角形,点 C 在正方形ABEF 外,在对角线 BF 上有一点 P,使 PC+PE 最小,则这个最小值的平方为( )
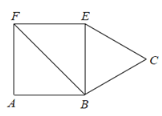
A.
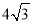 B.
B.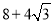 C.12D.
C.12D.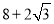
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.

-
科目: 来源: 题型:
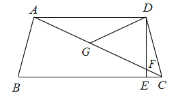
查看答案和解析>>【题目】如图,在四边形 ABCD 中,AD∥BC,DE⊥BC,垂足为点 E,连接 AC 交DE 于点 F,点 G 为 AF 的中点,∠ACD=2∠ACB,若 DC=5,则 AF 的长为___________.
相关试题

