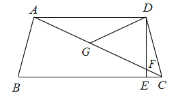
【题目】如图,在四边形 ABCD 中,AD∥BC,DE⊥BC,垂足为点 E,连接 AC 交DE 于点 F,点 G 为 AF 的中点,∠ACD=2∠ACB,若 DC=5,则 AF 的长为___________.
参考答案:
【答案】10
【解析】
根据直角三角形斜边上的中线的性质可得DG=AG,根据等腰三角形的性质可得∠GAD=∠GDA,根据三角形外角的性质可得∠CGD=2∠GAD,再根据平行线的性质和等量关系可得∠ACD=∠CGD,根据等腰三角形的性质可得CD=DG即可求解.
∵AD//BC,DE⊥BC,
∴AD⊥DE,
∵G为AF的中点,即DG为斜边AF的中线,
∴DG=AG=FG,
∴∠GAD=∠GDA,
∵AD//BC,
∴∠GAD=∠ACB,
设∠ACB=α,则∠ACD=2α,
∵∠GAD=∠GDA=α,
∴∠DGC=2α,即∠ACD=∠DGC,
∴DG=DC=5,
∴AF=10,
故答案为10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|2a﹣b+8|+(a+b﹣2)2=0.

(1)求a、b的值;
(2)如图1,点G在y轴上,三角形COG的面积是三角形ABC的面积的
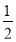 ,求出点G的坐标;
,求出点G的坐标;(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一个动点,连接OP、AC、DB,OE平分∠AOP,OF⊥CE,若∠OPD+k∠DOF=k(∠FOP+∠AOE),现将四边形ABDC向下平移
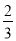 k个单位得到四边形A1B1D1C1,已知AM+BN =
k个单位得到四边形A1B1D1C1,已知AM+BN =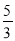 k,求图中阴影部分的面积.
k,求图中阴影部分的面积. -
科目: 来源: 题型:
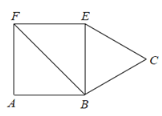
查看答案和解析>>【题目】如图,正方形 ABEF 的面积为 4,△BCE 是等边三角形,点 C 在正方形ABEF 外,在对角线 BF 上有一点 P,使 PC+PE 最小,则这个最小值的平方为( )
A.
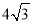 B.
B.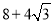 C.12D.
C.12D.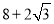
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形 ABCD 的对角线 AC=4,BD=2,以 AC 为边作正方形 ACEF,则 BF 的长为_____.
-
科目: 来源: 题型:
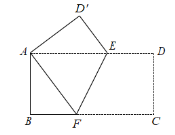
查看答案和解析>>【题目】如图,把一张长方形纸片 ABCD 折叠起来,使其对角顶点 A,C 重合,若其长 BC 为 9,宽 AB 为 3.
⑴求证:△AEF 是等腰三角形;
⑵EF= .
相关试题

