【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 坐标为
坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数的解析式和一次函数的解析式;
(2)连结![]() ,求
,求![]() 的面积;
的面积;
(3)观察图象直接写出![]() 时
时![]() 的取值范围是 ;
的取值范围是 ;
(4)直接写出:![]() 为
为![]() 轴上一动点,当三角形
轴上一动点,当三角形![]() 为等腰三角形时点
为等腰三角形时点![]() 的坐标 .
的坐标 .


参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)-2<x<0或x>3;(4)
;(3)-2<x<0或x>3;(4)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)利用待定系数法求出反比例函数的解析式,然后可得点B的坐标,再利用待定系数法求出一次函数的解析式即可;
(2)求出点D的坐标,根据两三角形面积和可得结论;
(3)写出一次函数图象在反比例函数图象上边时对应的x的取值范围即可;
(4)存在三种情况:OA=OP,OA=AP,AP=OP,根据点A的坐标结合图形可得点P的坐标.
解:(1)∵A的坐标是(3,1),
把A的坐标代入![]() 得:k=3,
得:k=3,
即反比例函数的解析式是![]() ,
,
把B(-2,m)代入反比例函数的解析式得:![]() ,
,
即B的坐标是![]() ,
,
把A、B的坐标代入y=ax+b得: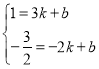 ,
,
解得:![]() ,
,![]() ,
,
即一次函数的解析式是![]() ;
;
(2)连接OB,
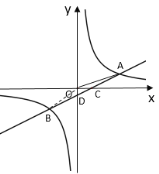
在![]() 中,当x=0时,
中,当x=0时,![]() ,即D(0,
,即D(0,![]() ),
),
∴![]() ,
,
∴ △AOB的面积=![]() ;
;
(3)由函数图象得:![]() 时
时![]() 的取值范围是-2<x<0或x>3;
的取值范围是-2<x<0或x>3;
(4)当△AOP是等腰三角形时,存在以下三种情况:
①当OA=OP时,如图2,
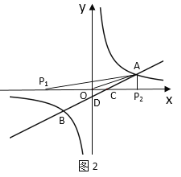
∵A(3,1),
∴OA=![]() ,
,
∴P1(![]() ,0)或P2(
,0)或P2(![]() ,0);
,0);
②当OA=AP时,如图3,
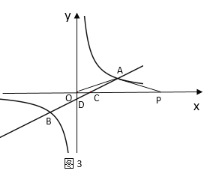
∵A(3,1),
∴P(6,0);
③当OP=AP时,如图4,过A作AE⊥x轴于E,
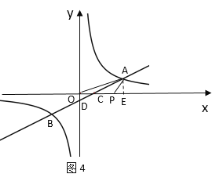
设OP=x,则AP=x,PE=3x,
∴AP2=AE2+PE2,即![]() ,
,
解得:![]() ,
,
∴P(![]() ,0);
,0);
综上,P的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级组织有奖知识竞赛,派小明去购买A、B两种品牌的钢笔作为奖品.已知一支A品牌钢笔的价格比一支B品牌钢笔的价格多5元,且买100元A品牌钢笔与买50元B品牌钢笔数目相同.
(1)求A、B两种品牌钢笔的单价分别为多少元?
(2)根据活动的设奖情况,决定购买A、B两种品牌的钢笔共100支,如果设购买A品牌钢笔的数量为n支,购买这两种品牌的钢笔共花费y元.
①直接写出y(元)关于n(支)的函数关系式;
②如果所购买A品牌钢笔的数量不少于B品牌钢笔数量的
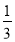 ,请你帮助小明计算如何购买,才能使所花费的钱最少?此时花费是多少?
,请你帮助小明计算如何购买,才能使所花费的钱最少?此时花费是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】参照学习函数的过程与方法,探究函数
 的图象与性质.
的图象与性质.因为
 ,即
,即 ,所以我们对比函数
,所以我们对比函数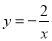 来探究.
来探究.列表:

…






1
2
3
4
…
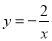
…

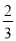
1
2
4


1


…

…


2
3
5


0


…
描点:在平面直角坐标系中,以自变量
p>(1)请你把 的取值为横坐标,以
的取值为横坐标,以 相应的函数值为纵坐标,描出了相应的点(如图所示).
相应的函数值为纵坐标,描出了相应的点(如图所示). 轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;(2)观察图象并分析表格,回答下列问题:
①当
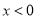 时,
时, 随
随 的增大而 ;(填“增大”或“减小”)
的增大而 ;(填“增大”或“减小”)②
 的图象是由
的图象是由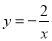 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;③
 图象关于点 成中心对称.(填点的坐标)
图象关于点 成中心对称.(填点的坐标)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
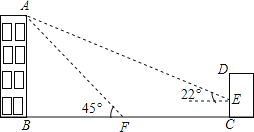
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈
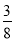 ,cos22°≈
,cos22°≈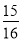 ,tan22°≈
,tan22°≈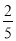 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|2a﹣b+8|+(a+b﹣2)2=0.

(1)求a、b的值;
(2)如图1,点G在y轴上,三角形COG的面积是三角形ABC的面积的
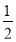 ,求出点G的坐标;
,求出点G的坐标;(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一个动点,连接OP、AC、DB,OE平分∠AOP,OF⊥CE,若∠OPD+k∠DOF=k(∠FOP+∠AOE),现将四边形ABDC向下平移
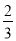 k个单位得到四边形A1B1D1C1,已知AM+BN =
k个单位得到四边形A1B1D1C1,已知AM+BN =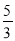 k,求图中阴影部分的面积.
k,求图中阴影部分的面积. -
科目: 来源: 题型:
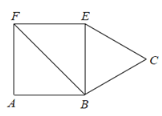
查看答案和解析>>【题目】如图,正方形 ABEF 的面积为 4,△BCE 是等边三角形,点 C 在正方形ABEF 外,在对角线 BF 上有一点 P,使 PC+PE 最小,则这个最小值的平方为( )
A.
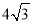 B.
B.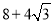 C.12D.
C.12D.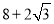
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.

相关试题

