【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
参考答案:
【答案】(1)0,-1),(0,-2),(0,0),(1,-1),(1,-2),(1,0),(2,-1),(2,-2),(2,0);(2)![]() .
.
【解析】
试题分析:(1)根据题意可得,x有三种等可能取值,即0,1,2;在每个取值下面,y都有三种等可能取值即:-1,-2,0,所以M点坐标共有9种等可能情况,分别是(0,-1),(0,-2),(0,0),(1,-1),(1,-2),(1,0),(2,-1),(2,-2),(2,0);(2)在上面这些9种等可能坐标中,有两个点的坐标即(1,0),(2,-1),在函数y=-x+1的图象上,故点M(x,y)在函数y=-x+1的图象上的概率P= ![]() .
.
试题解析:(1)通过列树形图可知,M点横坐标x有三种等可能取值,即0,1,2;在每个取值下面,纵坐标y都有三种等可能取值:即:-1,-2,0,所以M点坐标共有3×3=9种等可能情况,分别是(0,-1),(0,-2),(0,0),(1,-1),(1,-2),(1,0),(2,-1),(2,-2),(2,0);(2)在上面列举的9种等可能坐标中,其中在直线y=-x+1上的点是(1,0),(2,-1),∴点M(x,y)在函数y=-x+1的图象上的概率P= ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划购买20张课桌和一批椅子,该校了解到甲、乙两家商场以同样的价格出售同一型号的课桌与椅子,课桌报价200元/张,椅子报价50元/把.甲、乙两商场分别给出了不同的优惠方案.甲商场的优惠方案:凡买一张课桌赠送一把椅子;乙商场的优惠方案:所有课桌和椅子均按报价的九折销售.若该校需要
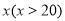 把椅子,在甲商场购买所花费用为
把椅子,在甲商场购买所花费用为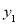 (元),在乙商场购买所花总费用为
(元),在乙商场购买所花总费用为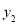 (元).
(元).(1)请分别写出
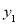 ,
,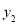 与
与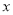 之间的函数关系式;
之间的函数关系式;(2)该校计划用8100元购买课桌和椅子,选甲、乙哪一家商场可以购买到尽可能多的椅子,说明理由;
(3)该校选择甲、乙哪一家商场花费较少?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF.
(1)求证:∠1+∠2=90°;
(2)如图2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH.
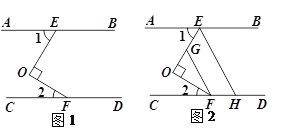
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
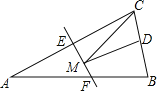
A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 若|a|=﹣a,则a<0
B. 式子3xy2﹣43x3y+12是七次三项式
C. 若a=b,m是有理数,则
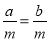
D. 若abcd<0,a+b=0,cd>0,那么这四个数中负因数的个数至少有1个
相关试题

