【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
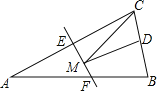
A.6B.8C.10D.12
参考答案:
【答案】C
【解析】
连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,由此即可得出结论.
解:连接AD,
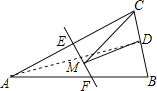
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=![]() BCAD=
BCAD=![]() ×4×AD=16,解得AD=8,
×4×AD=16,解得AD=8,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+![]() BC=8+
BC=8+![]() ×4=8+2=10.
×4=8+2=10.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 若|a|=﹣a,则a<0
B. 式子3xy2﹣43x3y+12是七次三项式
C. 若a=b,m是有理数,则
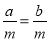
D. 若abcd<0,a+b=0,cd>0,那么这四个数中负因数的个数至少有1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B.
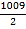 m2 C.
m2 C. 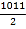 m2 D. 1009m2
m2 D. 1009m2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,
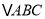 的三个顶点都在格点上,点
的三个顶点都在格点上,点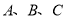 的坐标分别为
的坐标分别为 、
、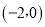 、
、 ,试解答下列问题:
,试解答下列问题:(1)画出
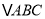 关于原点
关于原点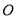 对称的
对称的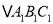 ;
;(2)平移
 ,使点
,使点 移到点
移到点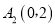 ,画出平移后的
,画出平移后的 并写出点
并写出点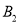 、
、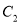 的坐标;
的坐标;(3)在
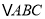 、
、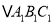 、
、 中,
中,  与哪个图形成中心对称?试写出其对称中心的坐标.
与哪个图形成中心对称?试写出其对称中心的坐标.
相关试题

