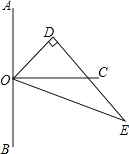
【题目】如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
参考答案:
【答案】(1)130°;(2)∠AOD与∠COE的差不发生变化,为30°;(3)∠AOE=131.25°或175°.
【解析】
(1)求出∠COE的度数,即可求出答案;
(2)分为两种情况,根据∠AOC=90°和∠DOE=60°求出即可;
(3)根据∠AOE=7∠COD、∠DOE=60°、∠AOC=90°求出即可.
(1)∵OC⊥AB,
∴∠AOC=90°,
∵OD在OA和OC之间,∠COD=20°,∠EOD=60°,
∴∠COE=60°-20°=40°,
∴∠AOE=90°+40°=130°,
故答案为:130°;
(2)在△ODE旋转过程中,∠AOD与∠COE的差不发生变化,
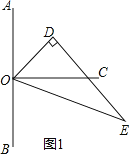
有两种情况:①如图1、∵∠AOD+∠COD=90°,∠COD+∠COE=60°,
∴∠AOD-∠COE=90°-60°=30°,
②如图2、∵∠AOD=∠AOC+∠COD=90°+∠COD,∠COE=∠DOE+∠DOC=60°+∠DOC,
∴∠AOD-∠COE=(90°+∠COD)-(60°+∠COD)=30°,
即△ODE在旋转过程中,∠AOD与∠COE的差不发生变化,为30°;
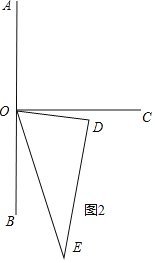
(3)如图1、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,
∴90°+60°-∠COD=7∠COD,
解得:∠COD=18.75°,
∴∠AOE=7×18.75°=131.25°;
如图2、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,
∴90°+60°+∠COD=7∠COD,
∴∠COD=25°,
∴∠AOE=7×25°=175°,
即∠AOE=131.25°或175°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写推理理由:
已知:如图,D,F,E分别是BC,AC,AB上的点,DF∥AB,DE∥AC,试说明∠EDF=∠A.

解:∵DF∥AB ( ),
∴∠A+∠AFD=180° ( ).
∵DE∥AC ( ),
∴∠AFD+∠EDF=180° ( ).
∴∠A=∠EDF ( ).
-
科目: 来源: 题型:
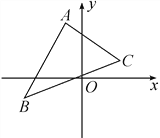
查看答案和解析>>【题目】如图,已知三角形ABC的三个顶点的坐标分别为A(-1,3),B(-3,-1),C(2,1),求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.
(1)画出△DEF;
(2)连接AD、BE,则线段AD与BE的关系是 ;
(3)求△DEF的面积.

-
科目: 来源: 题型:
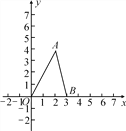
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(3,0).三角形AOB中任意一点P(x0,y0)经平移后的对应点为P1(x0+2,y0),并且点A,O,B的对应点分别为点D,E,F.
(1)指出平移的方向和距离;
(2)画出平移后的三角形DEF;
(3)求线段OA在平移过程中扫过的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某市城区地图(比例尺1∶9000)上,新安大街的图上长度与光华大街的图上长度分别是16 cm,10 cm.
(1)新安大街与光华大街的实际长度各是多少米?
(2)新安大街与光华大街的图上长度之比是多少?它们的实际长度之比呢?你发现了什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有( )
A. 2个B. 3个C. 4个D. 5个
相关试题

